[Survival Analysis] 생명표 방법
안녕하세요. 이번 포스트에서는 생존분석에 대해 다뤄드리도록 하겠습니다. 생존분석은 다른 데이터 분석들과 구분되는 큰 이유가 있는데요. 바로 중도절단 데이터를 이용한다는 점입니다. 이전에 Tobit Model 포스트에서 설명드린 바가 있듯이 Censored Data(검열 데이터)는 일반적인 통계 분석 방법을 사용하면 왜곡이 있을 수 있습니다. 따라서 어떻게 분석을 해야 하는지, 그리고 생존함수의 추정법 중 하나인 생명표 방법에 대해 소개해드리도록 하겠습니다.
개요
1. 생존분석
Tobit Model 포스트에서 0 이하 값에서 0으로 절단된 임금 데이터에 대해 소개해드린 바 있고, 이를 분석하기 위해 0 과잉 데이터 분석 모델인 Tobit Model에 대해 설명드렸습니다. 생존분석도 이와 비슷한 중도절단 데이터를 다루며 생존함수를 추정하거나 비교, 검정하는 분석 기법입니다. 생존분석은 의학, 보험, 금융 업계에서 주로 사용되지만, 부품 수명이 중요한 제조업에서도 많이 사용되고 있는 통계 분석 중 하나입니다.
아래 그래프와 같이 암환자의 수명을 관측하는 임상시험이 있다고 가정해 보겠습니다. 여기서 환자 1와 환자 4는 중도절단이 이뤄지지 않은 정상 데이터입니다. 환자 1은 연구 시작부터, 환자 4는 연구 도중에 참여했으나 연구 종료 전에 사망된 Case라고 볼 수 있습니다. 환자 2의 경우, 도중에 외국으로 가서 연락이 두절된 경우를 생각해볼 수 있습니다. 이 경우, 우리는 이 환자가 마지막으로 병원으로 왔던 진료시간까지만 살아있었음을 알 수 있고, 그 이후로 언제 사망했는지는 알 수가 없어서 정확한 생존시간을 알 수 없게 됩니다. 또는 환자가 암이 아닌 다른 질병이나 교통사고 등의 다른 원인으로 사망하게 된 경우에도 이 데이터는 불완전한 데이터가 됩니다.
환자 3과 같이 연구가 종료될 때까지 사망이 발생하지 않은 경우에도 이후에 얼마나 생존했는지를 알 수 없기 때문에 데이터가 중도절단 되었다고 합니다.
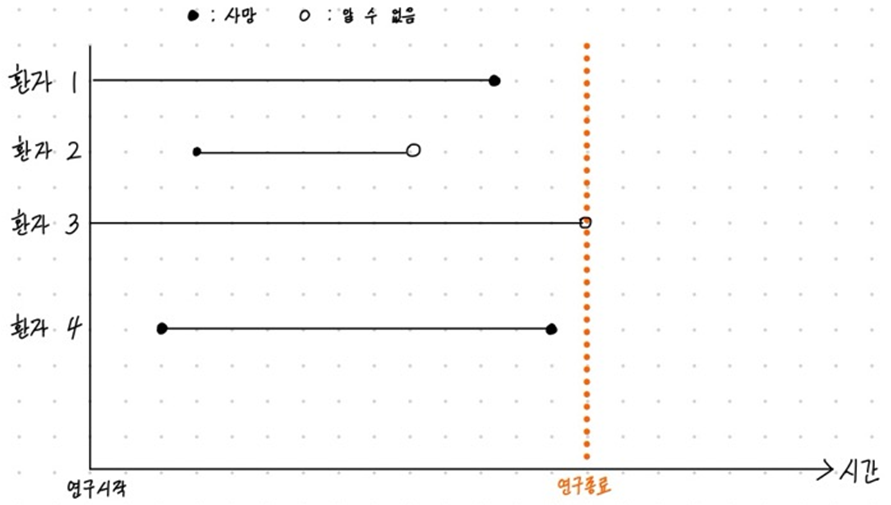
이렇듯 연구자에 의해 연구시간이 인위적으로 고정되거나, 연구자가 제어하지 못해 더 이상 연구 시간을 알 수 없는 데이터를 중도절단 데이터라고 합니다. 추가적으로 생존분석에서 필요한 생존함수에 대해 정의해보도록 하겠습니다. 생존시간을 $T$라고 하고 $T$가 확률밀도함수 $f(t)$와 분포함수 $F(t)$를 갖는다고 할 때, 생존함수는 환자가 $t$시간 이상 생존할 확률을 말하며 아래와 같이 나타냅니다.
$ \begin{align*} S(t) &= P(T>t) = 1 - F(t) \\ \end{align*} $
정의
2. 생명표 방법
그렇다면 이러한 중도절단을 포함하고 있는 데이터가 있을 때, 이 데이터에 대한 생존함수를 추정할 수 있는 방법 중 하나인 생명표 방법에 대해 말씀드리도록 하겠습니다. 생명표 방법은 특정 분포를 가정하지 않는 비모수적인 방법으로, 각각의 데이터의 생존시간을 고려하지 않고, 대신 생존시간을 집단 단위의 구간으로 나눠서 생존함수를 추정하는 기법입니다. 따라서, 가장 단순하고 직관적인 생존함수 추정 기법이고, 집단 단위의 생존분석에 적합합니다. 어떤 식으로 계산되는 것인지 예시를 먼저 말씀드리고, 일반화하여 정리해보도록 하겠습니다.
총 20명이 참여한 폐암 임상 실험이 있습니다. 아래는 연구 시작에서부터 1년 단위 구간별로 사망자 수와 중도 절단된 수를 나타낸 표입니다. 즉, 연구 시작부터 1년 안에 사망자 수는 2명 발생했으며, 중도 절단된 수는 0명임을 알 수 있습니다.
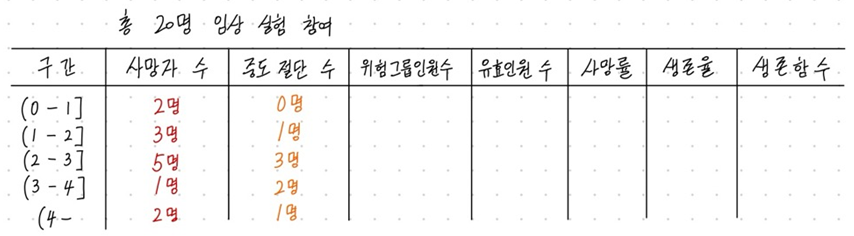
(0-1] 구간에서 사망 할 수 있는 위험이 발생할 수 있는 인원은 총 20명입니다. 즉, (0-1] 구간의 위험그룹인원수는 20명이 됩니다. 유효인원수는 위험그룹인원수에서 중도 절단 수의 절반을 뺀 값을 의미합니다. 생명표 방법에서는 중도절단된 환자들이 실제로 사망했는지 생존했는지는 모르지만, 평균적으로 구간의 반쯤만 사망위험에 노출됐다고 보자는 확률적인 해석을 하기 때문에 이와 같이 유효인원수로서 인원 수를 조정합니다. 이를 통해 중도절단 데이터도 모두 사망했다고 판단할 수 있는 위험 과대평가 혹은 중도절단 데이터를 무시하고 모두 생존했다고 가정하여 생존확률이 너무 높아지게 되는 위험 과소평가를 피할 수 있게 됩니다.
(0-1] 구간에서 중도 절단 수가 0명이므로 유효인원수도 20명이 되며, 사망률은 [(사망자 수 / 유효인원 수) = (2/20)]로 구해지게 됩니다. 생존율은 [1-사망률 = 0.9]이며, 따라서 생존함수는 [(전 구간까지 살아남은 확률) $\times$ (해당 구간의 생존율) = 1 $\times$ 0.9]로 구해집니다. 최종적으로 (0-1] 구간에서의 생명표는 아래와 같이 채워집니다.
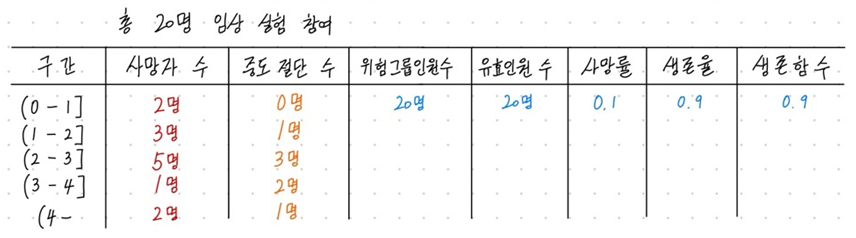
그렇다면 (1-2] 구간은 어떻게 계산될 지 보겠습니다. 위험그룹 인원 수는 전 구간의 사망자 수와 중도 절단 수의 합인 2명을 뺀 18명이 됩니다. 그리고 유효인원수는 위험그룹인원수인 18명에서 (1-2] 구간의 중도 절단 수인 1명의 절반을 뺀 17.5명이 됩니다. 사망률은 [(사망자 수 / 유효인원 수) = (3/17.5)]로 구해지게 되고, 생존율은 [1-사망률 = 0.829]가 됩니다. 생존함수는 [(전 구간까지 살아남은 확률) $\times$ (해당 구간의 생존율) = 0.9 $\times$ 0.829 = 0.746]으로 구해지게 됩니다. 아래는 위와 같은 방식으로 끝까지 진행했을 때, 최종 완성된 생명표입니다.

참고로 4년 이후부터는 연구가 종료되었으므로 생존함수를 고려하지 않습니다.
그렇다면 이를 일반화하여 수식으로 표현해보겠습니다.
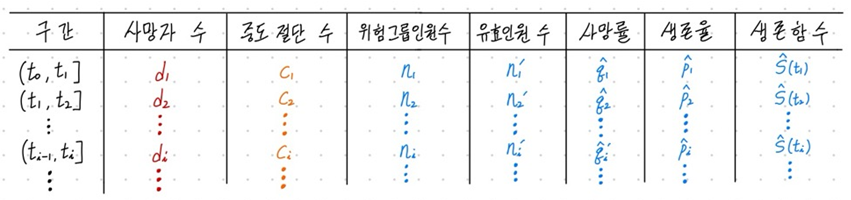
우선 위험그룹인원수 $n_{i}$는 $n_{i} = n_{i-1} - d_{i-1} - c_{i-1}$이며, 유효인원수는 위험그룹인원수에서 중도절단된 인원수의 절반을 뺀 $\grave{n_{i}} = n_{i} - c_{i} / {2}$가 됩니다. 사망률 $q_i$의 추정치는 $\hat{q_i} = d_{i} / \grave{n_{i}}$이 되고, 생존율 $p_i$의 추정치는 $\hat{p_i} = 1 - \hat{q_i} = 1 - d_{i} / \grave{n_{i}}$로 계산됩니다. 앞에서 생존함수는 [(전 구간까지 살아남은 확률) $\times$ (해당 구간의 생존율)]로 말씀드렸는데 왜 그런 것인지 아래와 같이 증명해보겠습니다.
$ \begin{align*} S(t_{i}) &= P(T > t_{i}) \\ &= P(T > t_{1})P(T > t_{2} | T > t_{1}) \cdots P(T > t_{i} | T > t_{i-1}) \\ &= p_{1}p_{2} \cdots p_{i} \\ \end{align*}$
즉, 생존함수의 추정치는 아래와 같이 구해질 수 있고, 연구 시작 구간부터 현재 구간까지의 생존율 추정값을 곱한 값이 생존함수 추정치가 됩니다.
$ \begin{align*} \hat{S}(t_{i}) &= \prod_{k = 1}^{i} \hat{p_{k}} \\ \end{align*}$
실습
생명표 방법을 통해 생존함수를 그릴 수 있습니다. 다만, Python 생존분석 패키지인 Lifelines 안에는 생명표 방법에 대한 함수가 따로 구현되어 있지 않기 때문에 생명표와 생존함수 그래프 시각화까지 직접 코드로 만들어보도록 하겠습니다.
-
생명표 만들기
위 함수를 통해 위험그룹인원수, 유효인원수, 사망률, 생존율, 생존함수 추정치 값들을 정리한 생명표를 생성할 수 있습니다.
import numpy as np
import pandas as pd
# 생명표 방법 함수 만들기
def life_table_method(times, censored, interval) :
# np.asarray : copy = False가 기본값
times = np.asarray(times)
censored = np.asarray(censored)
# 구간 나누기
max_time = times.max()
bins = np.arange(0, max_time + interval, interval)
normal_list = pd.cut(times[censored == 1], bins = bins)
censored_list = pd.cut(times[censored == 0], bins = bins)
# 정상 데이터와 중도절단 데이터의 Count 구하기
normal_counts = normal_list.value_counts().sort_index()
censored_counts = censored_list.value_counts().sort_index()
# 생명표 초안 만들기
temp = pd.DataFrame({
'Interval' : normal_counts.index.astype(str),
'Normal' : normal_counts.values,
'Censored' : censored_counts.reindex(normal_counts.index, fill_value = 0).values
})
# 생명표에 위험그룹인원수, 유효인원수, 사망률, 생존율, 생존함수 추가하기 위한 준비
n = len(times)
hazard_group_size_list = []
effective_sample_size_list = []
death_prob = []
survival_prob = []
survival_func = []
surv_func = 1.0
for idx, row in temp.iterrows() : # iterrows() : index과 row 값을 반환함.
d = row['Normal']
c = row['Censored']
n_i = n
# 유효인원수 계산
effective_sample_size = n_i - c / 2
# 사망률, 생존율, 생존함수 계산
q = d / effective_sample_size
p = 1 - q
surv_func *= p
# 사망률, 생존율, 생존함수 계산
hazard_group_size_list.append(n_i)
effective_sample_size_list.append(effective_sample_size)
death_prob.append(q)
survival_prob.append(p)
survival_func.append(surv_func)
# 위험그룹인원수 업데이트
n = n_i - d - c
temp['Hazard_group_size'] = hazard_group_size_list
temp['Effective_sample_size'] = effective_sample_size_list
temp['Death_prob'] = death_prob
temp['Survival prob'] = survival_prob
temp['Survival_func'] = survival_func
temp['Interval_start'] = [interval.left for interval in normal_counts.index]
temp = temp[: -1]
return temp
이전의 예시를 넣었을 때, 아래와 같은 생명표를 만들 수 있습니다.
times = [0.1, 0.2, 1.1, 1.2, 1.3, 1.4, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 3.1, 3.2, 3.3, 4.1, 4.2, 4.3]
censored = [1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0]
interval = 1
life_table = life_table_method(times, censored, interval)
life_table

- 생명표의 생존함수 추정치 그래프 시각화
생명표가 생성되었으면 이를 통해 생존함수 추정치에 대한 그래프를 그려볼 수 있습니다. 단, 생존시간을 집단 단위의 구간으로 정리했기 때문에 그래프로 step형태의 계단식으로 만들어지는 것이 특징입니다. 저는 일반적으로 plotly 시각화를 좋아하지만, plotly에는 step 계단형 그래프 전용 함수가 구현되어 있지 않기 때문에… 편의상 matplot을 이용하여 구현해 보았습니다.
import matplotlib.pyplot as plt
def life_table_survival_function_plot(table) :
# 마지막 생존함수 값도 수평선으로 끝나도록 조정
x = life_table['Interval_start'].tolist() + [life_table.loc[life_table.shape[0] - 1, 'Interval_start'] + 1]
y = life_table['Survival_func'].tolist() + [life_table.loc[life_table.shape[0] - 1, 'Survival_func']]
# where = 'post' : 생명표 그래프를 그리기 위한 조건 -> 수평선이 현재 x값 이후 구간에 적용
plt.step(x, y, where = 'post', linewidth = 2)
plt.title("Life Table Survival Function")
plt.xlabel("Time")
plt.ylabel("Survival Distribution Function")
plt.ylim(0, 1.05)
plt.grid(True)
plt.show()
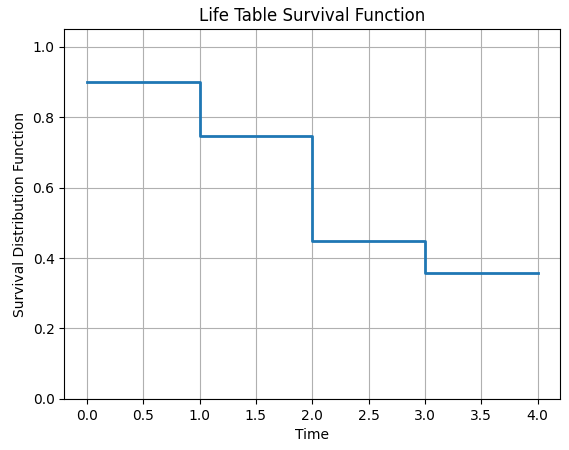
예시에서 만든 생명표를 이 함수에 넣었을 때 아래와 같은 생존함수 추정치 그래프를 만들 수 있습니다.
life_table_survival_function_plot(life_table)
Reference
- 통계분석방법론 수업 [이재원 교수님]
- 생명과학연구를 위한 통계적 방법 [이재원/박미라/유한나 지음]

댓글남기기