[Modeling] Knowledge Distillation
안녕하세요. 24년 새해가 밝았습니다! 😁 올해 첫 포스팅으로는 지식 증류라고 불리는 Know Distillation에 대해서 설명드리려고 합니다. 제작년 Dacon 대회에서 이 기법을 잘 이용해서 2위를 했었는데 어떻게 활용했었는지도 간단히 설명드리겠습니다. 저도 이번 기회에 더 자세히 알아보면서 새롭게 알게 된 내용들이 있었네요.
정의
최근에는 더 성능이 높은 머신러닝과 딥러닝 모형을 만들기 위해 더 복잡한 구조를 가져오거나 훨씬 많은 Parameter 수를 추가하고 있습니다. 이에 따라 상당한 양의 연산 처리가 필요해졌고, 메모리 한계, 추론 시간 증가 등의 문제가 발생하게 됩니다. 따라서 조금 더 실용적이고 빠르고 가벼우면서 성능을 뒤쳐지지 않는 모델의 필요성이 대두되었고, 모델 압축, 모델 구조 변경 등의 기법들이 등장했습니다. 이 중 지식 증류(Knowledge Distillation)는 알고리즘 경량화 기법 중 하나로, 잘 학습된 모델(Teacher model)의 지식을 받은 단순한 모델(Student model)을 통해 빠른 학습 시간과 높은 성능을 유지하는 기법입니다. 예시를 들어보겠습니다.
- Teacher model : 정확도 96%, 추론 시간 2시간
- Student model : 정확도 92%, 추론 시간 10분
정확도 96%의 성능 좋은 Teacher model이 있습니다. 그러나 시간이 2시간이나 걸려서 효율적이지 못합니다. 따라서, 이보다 간단한 모델인 Student model을 만들고, Teacher model의 지식을 이어 받습니다. 성능은 Teacher model보다 낮지만, 시간이 10분으로 빠르게 작동합니다. 이와 같은 기법을 Knowledge Distillation이라고 부릅니다.
특징
그렇다면 Teacher model의 지식을 Student model은 어떻게 받는 것일까요? 아래와 같이 4개의 음악 장르를 분류하는 모델이 있고, 특정 데이터에 대해 모델을 돌렸을 때를 가정해봅시다.
- 장르 : 4 범주 (Ballad, Dance, Hiphop, Classic)
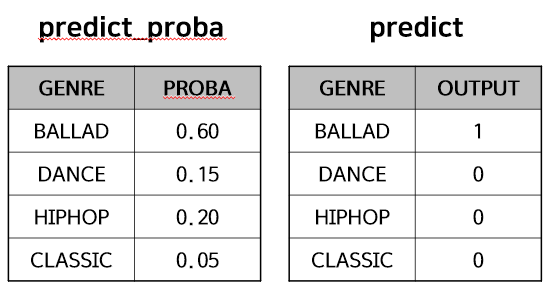
왼쪽 표는 예측결과의 확률분포로써 Soft Target이며, 오른쪽 표는 예측결과로 Hard Target이라고 합니다. 일반적으로 범주형 예측 모델에서 집중하는 부분은 Hard Target인 predict 값입니다. 보시다시피 해당 데이터는 BALLAD로 예측을 할 것입니다. 그러나 Hard Target으로는 각각 4개의 범주에 대한 예측확률에 대해서는 알지 못합니다. 예를 들어 BALLAD일 확률이 26%든, 99%든 OUTPUT이 1이라면 다 같은 BALLAD 예측값입니다. 하지만 어느 정도의 확률로 이 데이터를 BALLAD로 예측을 하는지에 대해서는 알지 못한다는 것입니다. Knowledge Distillation은 Teacher model의 지식을 Student model에 최대한 전달을 해줘야 하는 기법입니다. 당연히 Hard Target보다는 Soft Target이 더 많은 정보를 가지고 있습니다. 즉, Knowledge Distillation은 Soft Target에 집중합니다.
간단하게 Knowledge Distillation에 대해 도식화를 그려보았는데 이제 절차에 대해 설명드리겠습니다. 먼저 좋은 성능의 Teacher model을 학습시킵니다. 그리고 나서 Student model을 학습시키는데, 여기서 Student model의 종속변수($Y$) 값은 바로 Teacher model의 Soft Target입니다. Student model의 Soft Target이 예측되었다면 이를 통해 Hard Target을 만들고, 실제 $Y$과 비교하여 성능을 더 보완하도록 반복합니다.
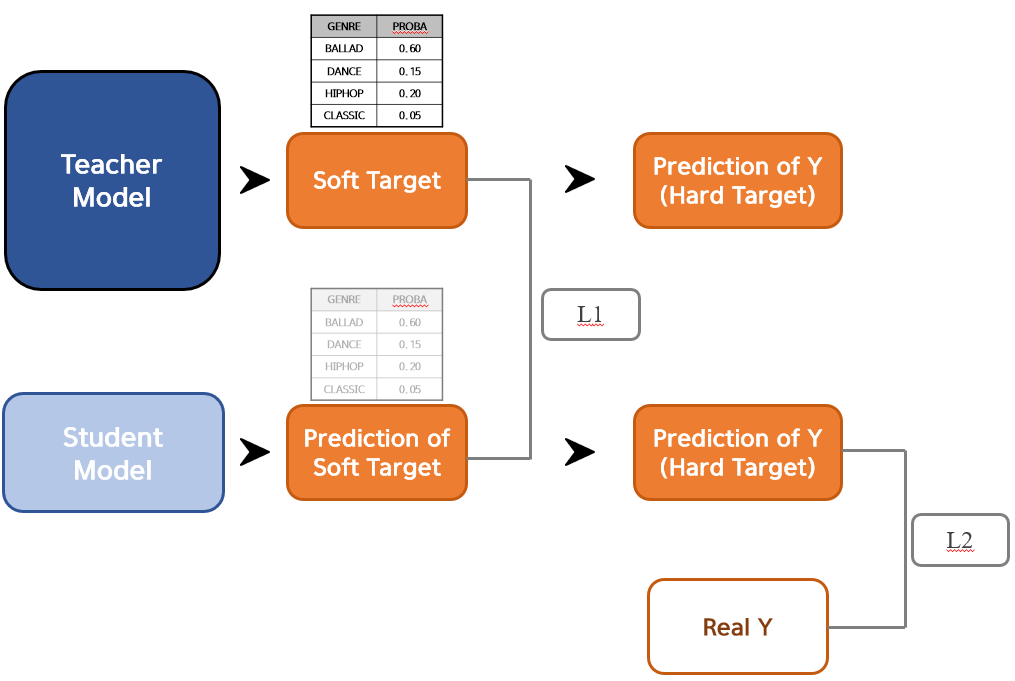
Knowledge Distillation에서 신경써야하는 Loss 값은 두 개입니다. Teacher model과 Student model의 Soft Target이 얼마나 비슷한지에 대한 $L_1$ 값, Student model의 Hard Target과 실제 Real Y 값과의 차이에 대한 $L_2$ 값이 그것입니다. 결론적으로 아래의 Loss를 최소로 만들도록 Student model이 학습됩니다.
$Student~~Loss = L_1 + \lambda \cdot L_2$
Knowledge Distillation도 ① Teacher model의 어떠한 지식을 전달할 것인지 ② Student model에 어떻게 전달할 것인지에 따라서 다양한 기법들이 존재합니다.
① Response-Based(반응변수 값), Feature-Based(설명변수 값), Relation-Based(반응변수 벡터 간의 관계와 구도)
② Offline-Distillation(오프라인), Online-Distillation(온라인), Self-Distillation(자가)
이 중 제가 앞에서 설명드린 지식 증류 기법은 Response-Based의 Offline-Distillation 입니다. 나머지 방법들에 대해서도 간단히 설명드리며 이에 대한 자세한 내용은 기회가 된다면 하겠습니다.
-
Feature-Based(설명변수 값) : Teacher model의 Feature(설명변수) Activation Boundary(Dicision boundary와 비슷한 개념)를 따르도록 학습
- Relation-Based(반응변수 벡터 간의 관계와 구도) : Teacher model의 Output 구조에 집중되도록 학습
- Online-Distillation(온라인) : 멀티 GPU를 통한 데이터 병렬처리와 더불어 복사된 네트워크끼리 서로 지식을 전달
- Self-Distillation(자가) : 하나의 네트워크 안에서 지식이 전달되면서 학습
실습
이제 실제로 제가 활용했었던 사례를 말씀드리겠습니다. 참여했던 대회는 Dacon 건설기계 오일 상태 분류 AI 경진대회이며, 운 좋게도 최종 2위를 기록했었습니다. 간단히 대회 개요에 대한 내용은 아래와 같습니다.
-
개요 : 건설장비에서 작동오일의 상태를 실시간으로 모니터링하기 위한 오일 상태 판단 이진 분류 모델 개발 (정상, 불량)
-
데이터 특징
- Train data : $(14095,$ $54$$)$
- Test data : $(6041,$ $19$$)$

이 대회의 가장 큰 특징은 Train data와 Test data의 Column 수가 다르다는 점이었습니다. 일반적으로 모델을 구축할 때, Train Set과 Test Set의 Column은 같아야 하고, 그렇지 않으면 오류가 발생합니다. 그래서 저는 Train Set과 Test Set에 모두 포함된 Column 18개 만으로 모델을 구축해보았었습니다. 그러나 Train Set의 기존 54개의 Column 중 18개만으로 모델을 구축하다보니 좋은 성능의 모델이 나오지 않았습니다. 따라서, 저는 ① Train Set의 많은 정보들을 통해 오일 상태를 정상과 불량으로 최대한 잘 분류해주는 Teacher model과 ② 이를 통해 도출된 결과값 predict_proba를 출력값으로 넣어서 Train Set의 기본 변수 18개만으로도 Teacher model을 잘 설명해줄 수 있는 Student model을 만들어 Knowledge Distillation을 적용했습니다.
그럼 이제 코드를 통해 설명드리겠습니다. EDA 및 통계 분석을 통해 최적의 성능을 발휘하는 Teacher model과 Student model의 입력 데이터 Shape은 아래와 같습니다.
- Teacher model
- 입력 : $(14095,$ $20$$)$ ; 기본 변수 18개 + 추가 변수 2개 (AL, BA)
- 출력 : $(14095,$ $1$$)$ ; Y_LABEL 변수
-
Student model
-
입력 : $(6041,$ $18$$)$ : 기본 변수 18개
-
출력 : $(6041,$ $1$$)$ ; Teacher model의 predict_proba 값
-
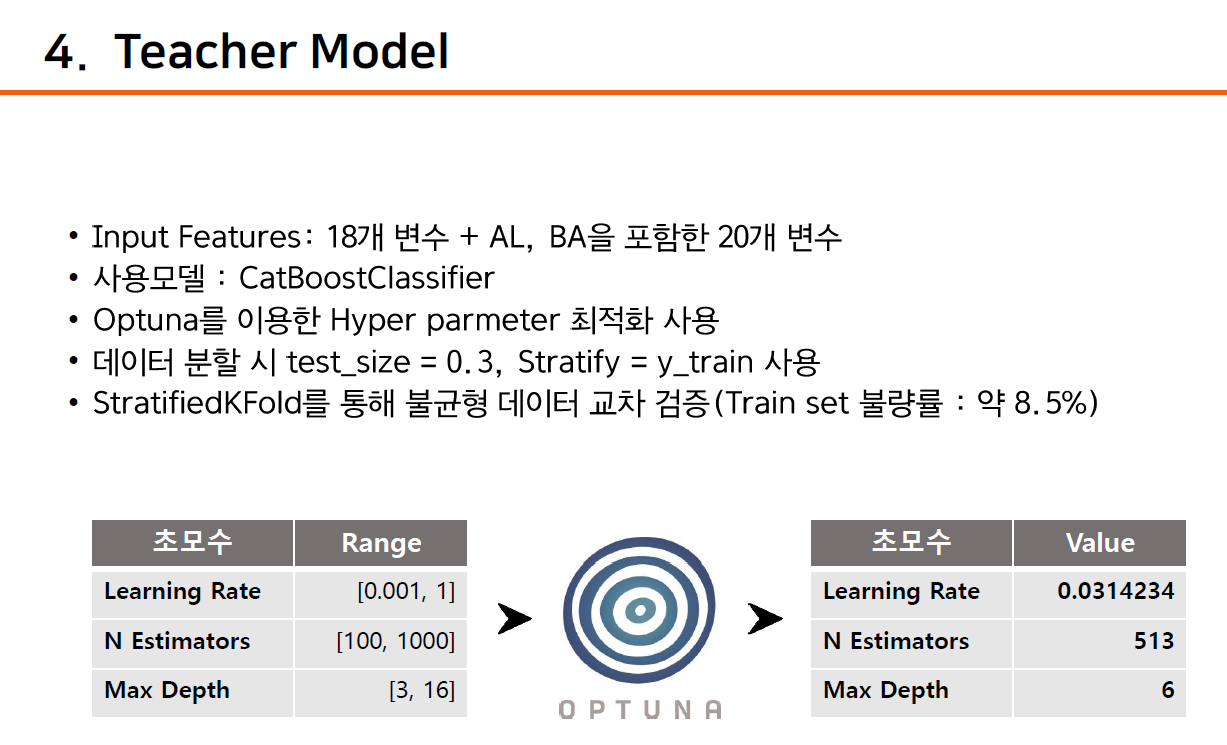
1. Teacher model
사용된 모델은 CatBoostClassifier이며, Obtuna를 통해 최적의 Parameter를 구한 후, 모델링을 구축합니다. cat_val과 같이 Teacher model의 proba 값을 구한 후, Student model의 출력값 데이터로 이용합니다.
# 교차 검증해서 얻은 초모수를 가지고 train 데이터의 예측 불량률을 파악한다.
n_fold = 5
cv = StratifiedKFold(n_splits = n_fold, shuffle = True, random_state = 39) # StrafitiedKFold로 데이터 분할하여 모델링
cat_val = np.zeros((X_train.shape[0], 2))
cat_partrain = np.zeros((X_partrain.shape[0], 2))
print(cat_val.shape)
print(cat_partrain.shape)
for i, (i_trn, i_val) in enumerate(cv.split(X_train, y_train), 1):
print(f'training model for CV #{i}')
optuna_cat = CatBoostClassifier( # CatBoostClassifier 모델 정의
random_state = 39,
learning_rate = 0.03142344166841527,
n_estimators = 513,
max_depth = 6)
optuna_cat.fit(X_train.loc[i_trn, :], y_train[i_trn], verbose = False, cat_features = categorical_features) # 모델링 실행
cat_val[i_val, :] = optuna_cat.predict_proba(X_train.loc[i_val, :]) # Teacher model의 predict_proba 값
cat_partrain += optuna_cat.predict_proba(X_partrain) / n_fold # Teacher model 성능 확인
print(cat_val.shape) # (14095, 2)
print(cat_partrain.shape) # (9866, 2)
train3['model1_prob'] = cat_val[:, 1]
print(train3.shape) # (14095, 22) -> 기본 변수 18개와 'model1_prob' 변수를 제외하고 모두 제거 예정
--------------------------------------------------------------------------------------------------------------------------------
(14095, 2)
(9866, 2)
training model for CV #1
training model for CV #2
training model for CV #3
training model for CV #4
training model for CV #5
(14095, 2)
(9866, 2)
(14095, 22)
2. Student model
출력값이 연속형이므로 사용된 모델은 CatBoostRegressor입니다. 역시 Optuna를 통해 최적의 Parameter를 구한 후, Train set을 이용하여 모델링을 구축합니다. 그리고 만들어진 모델에 바로 Test Set을 적용하여 성능을 도출했습니다.
# test 데이터의 예측 불량률 구하기
n_fold = 5
cv = KFold(n_splits = n_fold, shuffle = True, random_state = 39) # 출력값이 연속형이므로 KFold로 데이터 분할하여 모델링
cat_val = np.zeros((X_train2.shape[0]))
cat_test = np.zeros((X_test.shape[0]))
print(cat_val.shape)
print(cat_test.shape)
for i, (i_trn, i_val) in enumerate(cv.split(X_train2, y_train2), 1):
print(f'training model for CV #{i}')
optuna_cat = CatBoostRegressor( # 출력값이 연속형이므로 CatBoostRegressor 모델 정의
random_state = 39,
learning_rate = 0.01310047432090872,
n_estimators = 848,
max_depth = 9)
optuna_cat.fit(X_train2.loc[i_trn, :], y_train2[i_trn], verbose = False, cat_features = categorical_features) # 모델링 실행
cat_val[i_val] = optuna_cat.predict(X_train2.loc[i_val, :]) # Validation 성능
cat_test += optuna_cat.predict(X_test) / n_fold # Test 성능
--------------------------------------------------------------------------------------------------------------------------------
(14095,)
(6041,)
training model for CV #1
training model for CV #2
training model for CV #3
training model for CV #4
training model for CV #5

따라서, 아래와 같은 결과로 최종 2위를 기록할 수 있었습니다. 제가 사용한 기법은 Response-Based의 Offline-Distillation인데 추후 기회가 된다면 Knowledge Distillation의 다른 기법을 사용해 보고 싶네요!
Reference

댓글남기기