안녕하세요. 이번 시간에는 머신러닝 전에 종종 수행되는 Sampling 기법에 대해 알아보겠습니다. 그 중 UnderSampling에 대해 이번에 포스팅하겠으며, 다음 번에 OverSampling과 Mixed Sampling에 대해서 정리하도록 하겠습니다. 왜 Sampling을 수행해야 하는지, 어떤 경우에 수행해야 하는지, 그리고 6가지의 UnderSampling 기법들에 대하여 설명하겠습니다.

개요

머신러닝 분류 모델에서 가장 큰 적 중 하나는 불균형 자료입니다. 불균형 자료를 그대로 분류 모델에 적용했을 때, 제대로 된 성능이 나오기 어렵기 때문입니다. 특히, 금융업계의 고객 신용 데이터가 대개 불균형 자료입니다. 예를 들어, 어느 금융회사의 고객들을 살펴보았을 때, 정상 고객이 97%, 신용 불량 고객이 3%라고 가정해봅시다. 이 상태에서 일반적인 머신러닝 모델을 만든다면 새로 들어오는 데이터들을 모두 정상으로 판정할 가능성이 있습니다. 왜냐하면 모두 정상이라고 판단을 하더라도 그 정확도는 실제로 불량 고객인 3%를 제외한 97%이기 때문입니다. 즉, 불량 고객 데이터가 너무 적기 때문에 새로 들어오는 모든 데이터를 정상이라고 판정하더라도 높은 성능의 모델이 만들어지면서, 실제로 정말로 좋은 성능의 모델이 만들어지지 않을 가능성이 높습니다.

이러한 불균형 자료의 문제를 해결하는 방법은 데이터를 Resampling하는 것입니다. 데이터 종속변수 Y의 각각 집단의 수량을 맞추는 것을 의미하는데 크게 3가지 방법이 있습니다. 다수 집단의 수량을 줄이는 UnderSampling(과소 표집 샘플링), 소수 집단의 수량을 늘리는 OverSampling(과대 표집 샘플링), 그리고 앞선 두 가지의 방법을 혼합한 Mixed Sampling(복합 샘플링)입니다.

UnderSampling의 장점은 데이터 수가 줄어들기 때문에 분석 시간이 짧아진다는 것입니다. 그러나 데이터의 수를 줄이기 때문에 정보 손실로 인해 모형의 정밀도가 떨어진다는 큰 단점을 가지고 있습니다. 따라서 일반적으로 불균형자료에서는 OverSampling이 더 많이 쓰이고 있습니다. 이제 UnderSampling 6가지 기법에 대해 소개해드리도록 하겠습니다.


실습

0. DataSet 소개

데이터는 sklearn에 내장된 데이터셋인 make_classification을 사용했습니다. 가상의 분류모형 데이터셋으로 특성변수 10개, 클래스 3개로 이루어져있습니다.

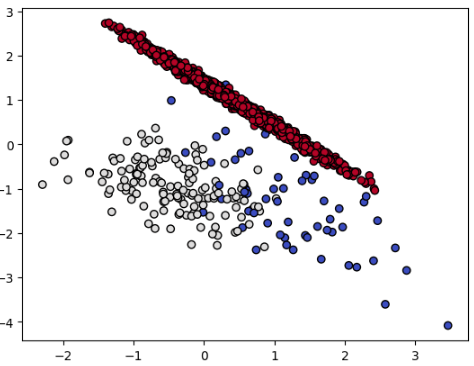
10개의 특성변수 중 0번째와 1번째 특성변수를 그래프로 나타내보았고, 3개의 클래스의 분포를 보았을 때 한쪽 클래스(빨강 점)로 쏠려있는 것을 볼 수 있습니다.

(2번 클래스 개수 : 총 2000개 중 1795개)

  • 데이터 특징
    • Shape : $(2000, 10)$
    • class : {$2$(빨강 점)$: 1795, ~~$$1$(흰 점)$: 141, ~~$$0$(파랑 점)$: 64$}
from collections import Counter
from sklearn.datasets import make_classification # dataset -> sklearn에 내장되어 있는 데이터 셋
import matplotlib.pyplot as plt

X, y = make_classification(n_classes = 3, weights = [0.03, 0.07, 0.9], n_features = 10,
            n_clusters_per_class = 1, n_samples = 2000, random_state = 10) # 특성변수 10개, 클래스 3개
print('Original dataset shape %s' % Counter(y))

plt.scatter(X[:, 0], X[:, 1], marker = 'o', c = y,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Original dataset shape Counter({2: 1795, 1: 141, 0: 64})

image-20240803163615562


1. Random UnderSampling

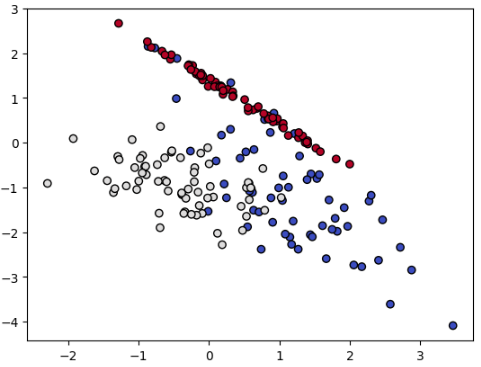
먼저 Random UnderSampling입니다. 말 그대로 무작위로 샘플링을 하는 기법입니다. 클래스 3개 중 가장 적은 수의 클래스는 0번 클래스로 64개의 데이터를 가지고 있습니다. 따라서, 다른 두 클래스의 데이터는 무작위로 64개를 추출하고, 나머지는 삭제됩니다. 아무런 제약 없이 무작위로 추출하기 때문에 시간이 빠르다는 장점이 있지만, random_state에 따라 결과가 달라지기 때문에 각 클래스의 분류 경계면의 변동이 크다는 단점을 가지고 있습니다.

from imblearn.under_sampling import RandomUnderSampler

X_us, y_us = RandomUnderSampler(random_state = 2024).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_us))

plt.scatter(X_us[:, 0], X_us[:, 1], marker = 'o', c = y_us,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({0: 64, 1: 64, 2: 64})

image-20240803170027518


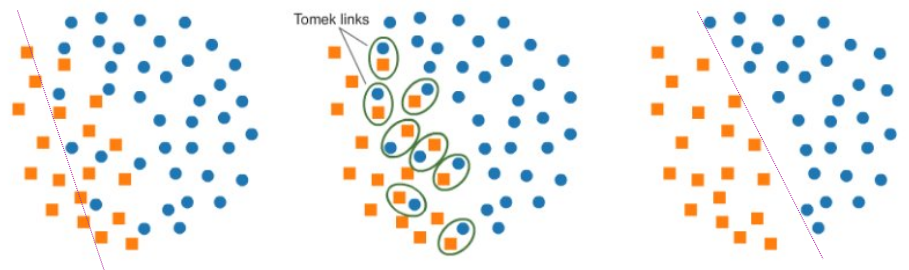
다음으로 Tomik Links입니다. 이 기법을 설명하기 전에 먼저 Tomik Links에 대한 정의를 설명하겠습니다. 서로 다른 범주에서 하나씩 추출한 데이터를 각각 $x_i, x_j$라고 하고 어느 두 점간의 유클리디안 거리를 $d$라고 할 때, $k \neq i, j$에 대하여 $d(x_i, x_k) < d(x_i, x_j)$ 또는 $d(x_j, x_k) < d(x_i, x_j)$가 성립되는 관측치 $x_k$가 없는 경우, 두 sample $x_i$와 $x_j$를 Tomik Links를 형성한다고 합니다. 쉽게 말해 아래 그림과 같이 서로 다른 두 클래스에서 추출한 두 sample의 거리가 두 sample 중 한 sample을 다른 점으로 두었을 때의 거리보다 항상 짧다면 두 sample을 Tomik Links라고 정의합니다.

이렇듯 여러 쌍의 Tomik Links을 찾아낸 후, 각 한 쌍의 데이터 중 다수 클래스인 데이터를 삭제하여 UnderSampling하는 기법입니다. 이 기법은 아래와 같이 분류 경계를 더 명확하게 만드는 효과가 있어 정보의 유실을 줄일 수 있지만, 제거되는 샘플이 Tomek links에 해당되는 데이터만으로 한정되어 크게 UnderSampling의 효과를 보지 못한다는 점이 단점입니다. 또 하나의 특징으로 분류 경계면이 다수 클래스 쪽으로 이동되는 효과가 있습니다.

image-20240803174806741

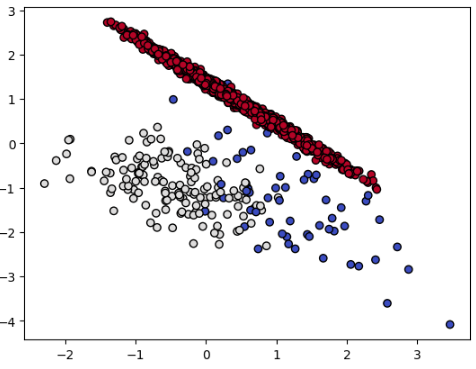
보다시피 2번 클래스에서 1795개의 중 4개의 점만 삭제되어 UnderSampling의 효과가 거의 없는 것을 볼 수 있습니다.

from imblearn.under_sampling import TomekLinks

tl = TomekLinks()
X_tl, y_tl = tl.fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_tl))

plt.scatter(X_tl[:, 0], X_tl[:, 1], marker = 'o', c = y_tl,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1791, 1: 141, 0: 64})

image-20240803170205564


3. CNN(Condensed Nearest Neighbor)

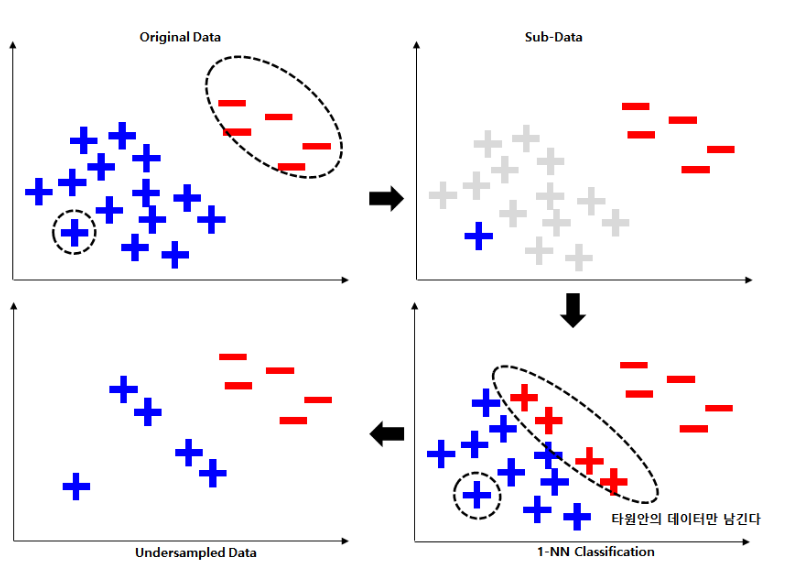
CNN(Condensed Nearest Neighbor)은 KNN(K = 1) 기법을 사용한 UnderSampling입니다. 아래 그림을 살펴보겠습니다.

여기 다수 클래스의 파란색 플러스와 소수 클래스의 빨간색 마이너스 데이터가 있습니다. 먼저 무작위로 다수 클래스의 데이터 중 하나를 선택하고, 소수 클래스의 데이터는 모두 선택하여 Sub-Data를 구성합니다. 그리고 Sub-Data를 이용하여 Original Data를 KNN(K = 1) 분류합니다. 이때, 다수 클래스를 다수 클래스로 정확히 분류한 데이터는 제거하고, 다수 클래스를 소수 클래스로 잘못 분류한 데이터들을 남기면서 UnderSampling이 진행됩니다.

즉, 다수 클래스를 다수 클래스로 정확히 분류한 데이터를 제거한다는 것은 머신 러닝 예측을 다수 클래스 쪽으로 쏠리게 하는 데이터를 제거한다는 의미로서, 남아있는 다수 클래스과 소수 클래스의 학습으로 모델링의 성능을 높이는 기법이라고 할 수 있습니다.

image-20240803175112838

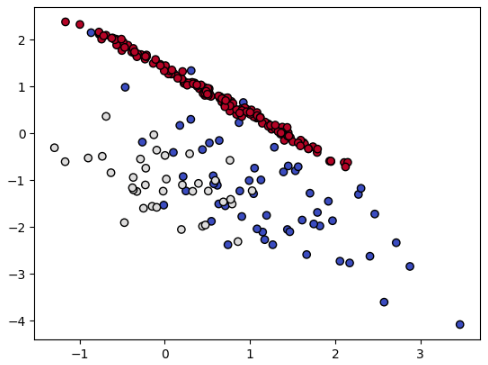
2번 클래스가 149개로 크게 UnderSampling 된 것을 볼 수 있습니다. 더불어서 1번 클래스는 37개로 기존 소수 클래스인 0번 클래스보다 더 줄어든 것을 볼 수 있습니다.

from imblearn.under_sampling import CondensedNearestNeighbour

X_cnn, y_cnn = CondensedNearestNeighbour(random_state = 10).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_cnn))

plt.scatter(X_cnn[:, 0], X_cnn[:, 1], marker = 'o', c = y_cnn,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 149, 0: 64, 1: 37})

image-20240803180012318


4. OSS(One sided Selection)

OSS(One sided Selection)는 앞서 설명한 Tomik Links와 CNN 기법을 결합한 기법입니다.

Tomik Links를 통해 분류 경계면의 다수 클래스 데이터를 제거하고, CNN으로는 분류 경계면에서 멀리 떨어진 다수 클래스 데이터를 제거하는 기법입니다. 즉, 두 기법의 단점을 보완하면서 균형있는 데이터를 생성합니다.

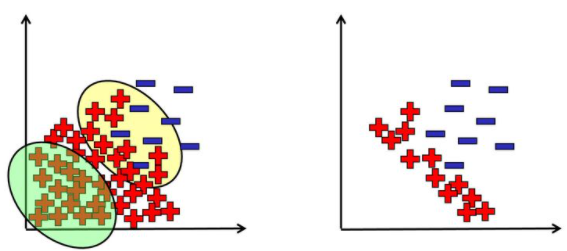
image-20240803180515133

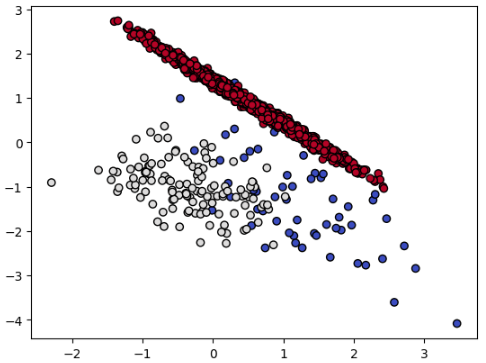
그러나 아래 결과와 같이 생각보다 UnderSampling이 일어나지 않았습니다. (random_state를 바꿔보았지만 데이터가 생각보다 줄어들지 않네요)

from imblearn.under_sampling import OneSidedSelection

X_oss, y_oss = OneSidedSelection(random_state = 10).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_oss))

plt.scatter(X_oss[:, 0], X_oss[:, 1], marker = 'o', c = y_oss,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1669, 1: 124, 0: 64})

image-20240803180549747


5. ENN(Edited Nearest Neighbours)

ENN(Edited Nearest Neighbours)도 KNN 기법을 이용한 UnderSampling입니다. 이 기법은 kind_sel 인자의 값에 따라 결과가 달라집니다. 다수 클래스 데이터 중 거리상 가장 가까운 k개(n_neighbors)의 데이터를 확인하는데 이때, kind_sel = "all"이라면 k개 데이터의 데이터 중 하나라도 다수 클래스가 아닐 경우, kind_sel = "mode"라면 절반 이상의 데이터가 다수 클래스가 아닐 경우에 삭제됩니다. 그러므로 kind_sel = “all”일 경우가 “mode”일 경우보다 더 많이 UnderSampling 됩니다. 이 방법도 분류 경계면을 다수 클래스 쪽으로 이동시키지만 데이터가 많이 제거되지는 않는 기법입니다.

kind_sel 인자에 따라 아래와 같이 결과가 달라집니다.

  • Raw Data : {2: 1795, 1: 141, 0: 64}

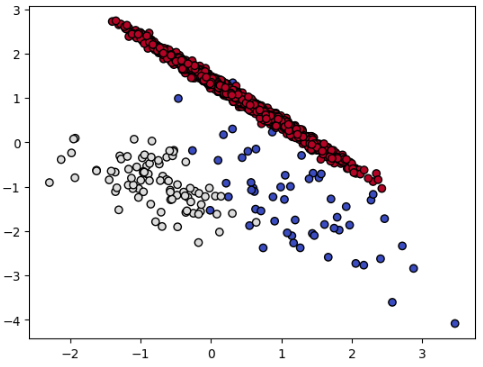
  • kind_sel = “all” : {2: 1734, 1: 86, 0: 64}
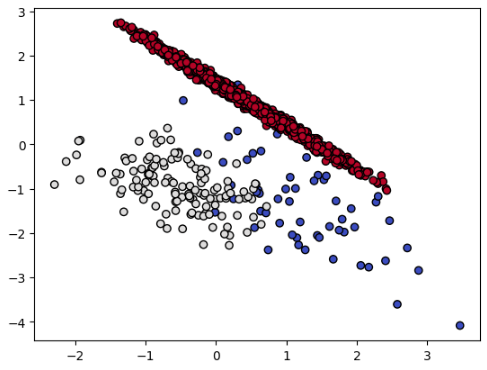
  • kind_sel = “mode” : {2: 1795, 1: 127, 0: 64} (거의 UnderSampling 되지 않음)
# kind_sel = "all"
from imblearn.under_sampling import EditedNearestNeighbours

X_enn1, y_enn1 = EditedNearestNeighbours(kind_sel = "all", n_neighbors = 5).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_enn1))

plt.scatter(X_enn1[:, 0], X_enn1[:, 1], marker = 'o', c = y_enn1,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1734, 1: 86, 0: 64})

image-20240803183051161

# kind_sel = "mode"
from imblearn.under_sampling import EditedNearestNeighbours

X_enn2, y_enn2 = EditedNearestNeighbours(kind_sel = "mode", n_neighbors = 5).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_enn2))

plt.scatter(X_enn2[:, 0], X_enn2[:, 1], marker = 'o', c = y_enn2,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1795, 1: 127, 0: 64})

image-20240803184344075

6. NCL(Neighbourhood Cleansing Rule)

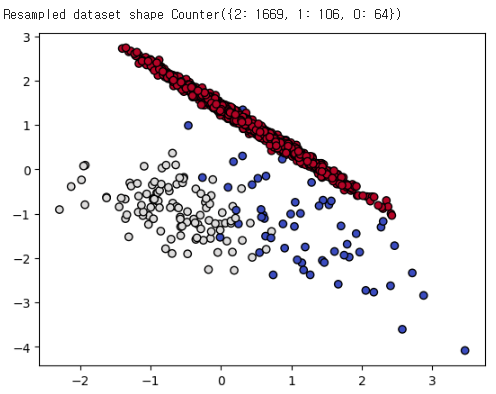
마지막 NCL(Neighbourhood Cleansing Rule)입니다. (개인적으로는 영어 문구상 NCR이어야 할 것 같은데 NCL이네요…) 이 기법은 CNN과 ENN을 결합한 기법입니다. 현재 kind_sel 인자는 deprecated 되버려서 항상 kind_sel = “all”로 적용한다고 합니다.

from imblearn.under_sampling import NeighbourhoodCleaningRule

X_ncl, y_ncl = NeighbourhoodCleaningRule(n_neighbors = 5).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_ncl))

plt.scatter(X_ncl[:, 0], X_ncl[:, 1], marker = 'o', c = y_ncl,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()

image-20240803185458058


다음 포스팅에는 OverSampling에 대하여 정리하도록 하겠습니다.


Reference

  1. cjkangme.log
  2. DATA NOTE
  3. 파이썬을 이용한 통계적 머신러닝    [박유성 지음]
  4. shinminyong
  5. cleansky.log
  6. 데이터 사이언스 스쿨
  7. Taegu


DATA_100%_LOGO_LIGHT



댓글남기기

참고

[연속형 분포] 코시 분포

안녕하세요! 최근 AI 기법들에 대해 설명 드렸었는데 잠시 쉬어가는 의미로 오랜만에 수리통계학 분포 시리즈로 돌아왔습니다. 올해 마지막 포스팅으로 코시 분포에 대해 설명드리도록 하겠습니다.

[Anomaly Detection] Isolation Forest

안녕하세요! 이번 시간에도 지난 포스트에 이은 Anomaly Detection 포스트입니다. 모델 기반 Anomaly Detection 기법 중 하나인 Isolation Forest에 대해 알아보도록 하겠습니다. 언뜻보면 Random Forest와 비슷한 부분도 있지만, 목적은...

[Anomaly Detection] LOF

이번 시간부터는 드디어 Anomaly Detection으로 넘어가보도록 하겠습니다. 평소에 이상탐지에 관심이 많았는데 재밌고 새로운 사실도 알게되서 너무 좋네요! 😄 Anomaly Detection 파트의 첫 번째 시간이기 때문에 간단히 이상탐지에 대해 알아보고, 밀도 기반 이...

[Sampling] Mixed sampling

이번 시간에는 Sampling의 마지막 포스트인 Mixed Sampling에 대해 알아보겠습니다. 즉, 앞서 설명드린 UnderSampling과 OverSampling을 모두 이용하는 Sampling 기법입니다. 간단히 2가지 정도를 소개하고 Sampling Chapter를 마...