안녕하세요. 지난 포스트인 UnderSampling에 이어서 Sampling 기법 중 하나인 OverSampling에 대해 알아보겠습니다. 일반적으로 머신러닝에서 UnderSampling보다 많이 사용되며, 4가지 정도 소개하도록 하겠습니다.

개요

다수 집단 데이터를 제거하는 Sampling 기법이 UnderSampling이라면 소수 집단 데이터를 늘리는 Sampling 기법이 바로 OverSampling(과대 표집 샘플링)입니다. UnderSampling은 표본 수를 줄이기 때문에 모델의 정밀도가 일반적으로 떨어집니다. 따라서, OverSampling을 사용하는 것이 통계적으로 유의합니다. 주요 기법으로는 SMOTE와 ADASYN이 있는데 이들을 포함한 4가지 기법에 대해서 아래와 같이 소개드리도록 하겠습니다.


실습

0. DataSet 소개

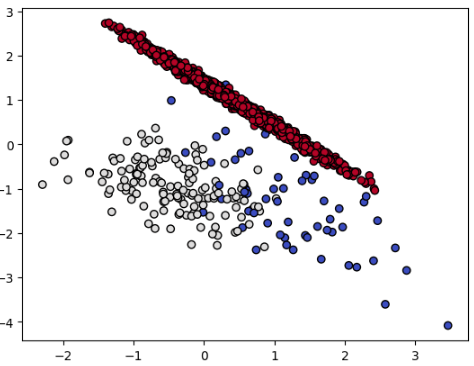
데이터는 지난 포스트인 UnderSampling에서 사용한 make_classification에서 가져왔습니다. 10개의 특성변수 중 0번째와 1번째 특성변수를 그래프로 나타내보았습니다.

  • 데이터 특징
    • Shape : $(2000, 10)$
    • class : {$2$(빨강 점)$: 1795, ~~$$1$(흰 점)$: 141, ~~$$0$(파랑 점)$: 64$}
from collections import Counter
from sklearn.datasets import make_classification # dataset -> sklearn에 내장되어 있는 데이터 셋
import matplotlib.pyplot as plt

X, y = make_classification(n_classes = 3, weights = [0.03, 0.07, 0.9], n_features = 10,
            n_clusters_per_class = 1, n_samples = 2000, random_state = 10) # 특성변수 10개, 클래스 3개
print('Original dataset shape %s' % Counter(y))

plt.scatter(X[:, 0], X[:, 1], marker = 'o', c = y,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Original dataset shape Counter({2: 1795, 1: 141, 0: 64})

image-20240803163615562


1. Random OverSampling

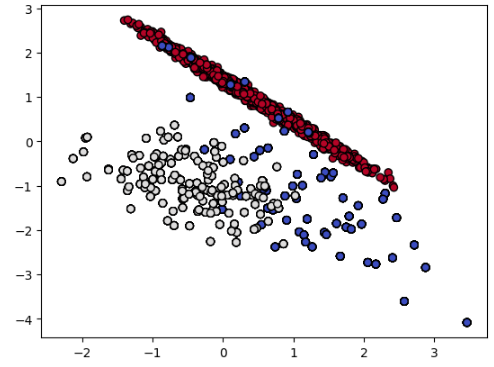
첫 번째로 Random OverSampling입니다. 소수 클래스의 데이터를 무작위로 복제하여 과대표집하는 기법입니다. 즉, 같은 값의 소수 클래스 데이터가 만들어지는 기법입니다. 물론 장점은 UnderSamplling보다 데이터가 많기 때문에 모델의 성능은 뛰어날 수 있지만, 소수 클래스 데이터 예측을 할 때, 상당한 Overfitting이 발생할 가능성이 높습니다. 똑같은 값으로 만들어진 소수 클래스의 데이터가 그대로 모델로 학습되기 때문입니다. 또한, 무작위로 복제를 하는 것이기 때문에 일부 소수 클래스 데이터는 많이 복제되고, 다른 소수 클래스 데이터는 적게 복제되어, 모델 성능이 떨어질 수 있습니다.

아래 그래프를 보았을 때, 파란색 동그라미가 빨간색 동그라미 위로 올려지게 그려진 것을 일부 볼 수 있는데, 소수 클래스 데이터가 복제되었다는 것을 알 수 있습니다. 다만, 소수 클래스의 값을 그대로 복제한 것이기 때문에 그래프로 보았을 때는 파란색과 하얀색 동그라미 개수가 빨간색만큼 늘어나보이지 않습니다. 아마 여러 개의 파란색과 하얀색 동그라미가 겹쳐져서 그려졌기 때문에 수가 적어 보일 것입니다.

from imblearn.over_sampling import RandomOverSampler

X_os, y_os = RandomOverSampler(random_state = 2024).fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y_os))

plt.scatter(X_os[:, 0], X_os[:, 1], marker = 'o', c = y_os,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})

image-20240907120459839


2. SMOTE

다음으로 주로 사용되는 기법 중 하나인 SMOTE입니다. 일명 합성소수표집법(Systhetic Minority Oversampling Technique)으로 불리는 기법으로, K-nearest neighbors에 대한 이해가 필요합니다. K-nearest neighbors는 어느 특정 데이터 주변의 K개의 가장 가까운 데이터를 의미합니다. 이를 이용하여 아래와 같이 진행됩니다.

  1. 소수클래스 주변의 몇 개의 데이터를 K-nearest neighbors로 정할지, $k$값을 정합니다.

  2. 소수클래스 데이터 중 하나인 관측치 $x_i$에 대해 K-nearest neighbors 셋인 $S_i$를 생성합니다.

    단, K-nearest neighbors는 모두 소수클래스 데이터여야만 합니다.

  3. 새로운 관측치 $x_{syn}$은 아래의 식으로 생성됩니다.

    $x_{syn} = x_i + \lambda(x_k - x_i)$

    여기서 $x_k$는 K-nearest neighbors 셋인 $S_i$에서 임의로 뽑은 소수클래스 데이터이고,

    $\lambda$는 $0\sim1$의 값으로 균등분포에서 임의로 추출한 값입니다. -> 즉, 0과 1사이에서 무작위로 추출한 값입니다.

  4. 이 절차를 소수클래스에 속한 모든 관측치에 대해 반복적으로 실시합니다.

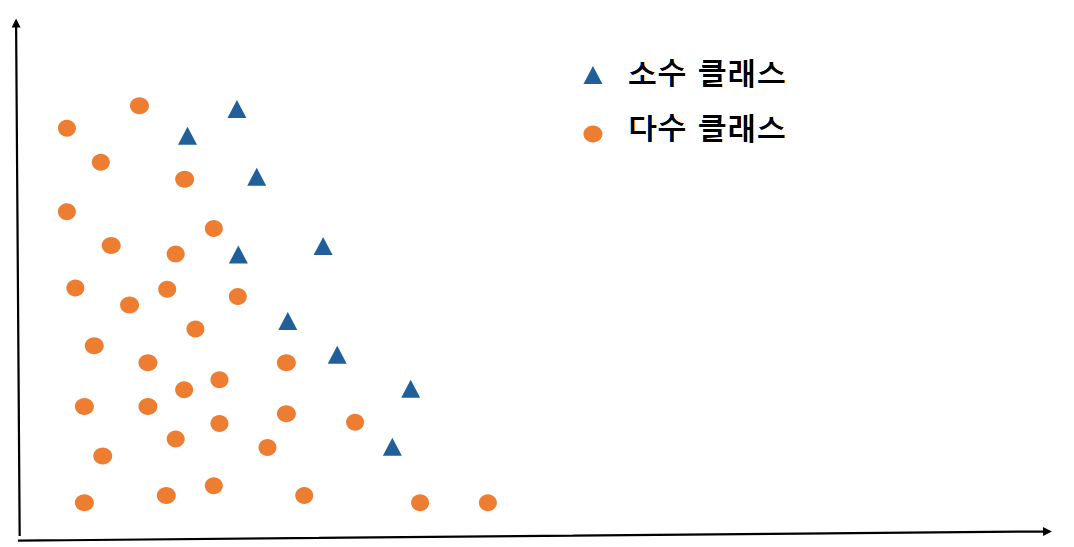
사실 글로써만 말씀드리면, 어떻게 만들어지는지 잘 모르실 것 같아서, 그림을 준비해보았습니다. 아래와 같이 동그라미 데이터는 다수 클래스, 세모 데이터는 소수 클래스를 의미합니다.

image-20240907144403820

  1. K-nearest neighbors $k$값 정하기

    : $k$ 값은 $5$로 정해보겠습니다.

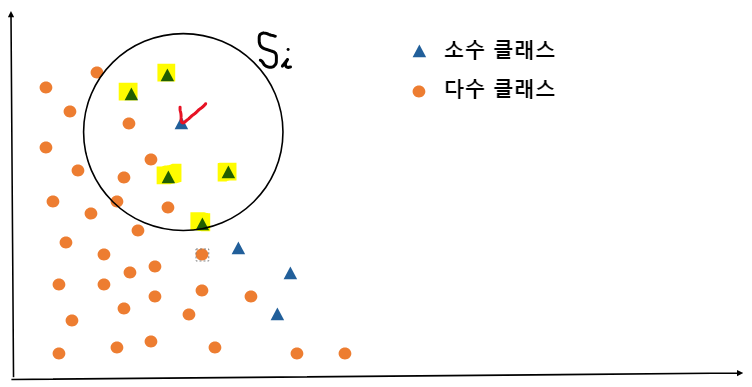
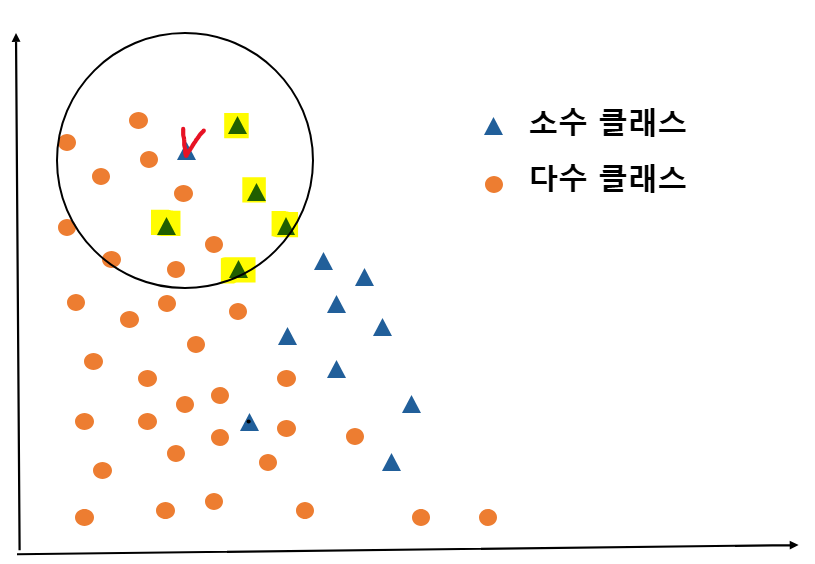
  2. 소수 클래스 데이터 중 체크 표시한 데이터의 K-nearest neighbors 셋인 $S_i$를 구합니다.

    아래 그림과 같이 체크 표시한 데이터 주변의 소수 클래스 데이터 5개를 둘러싼 원인 $S_i$가 그려집니다.

    image-20240907142958811

  3. 저 5개의 소수 클래스 데이터 중 한 개를 임의로 정합니다. -> 저는 파란색 체크표시한 데이터로 정했습니다.

    그리고 파랑 체크 데이터와 빨강 체크 데이터 사이에 가상의 선분을 그렸을 때, 선분 위 점들 중 무작위로 한 개의 점을 찍어 $x_{syn}$를 생성합니다.

    $x_{syn} = x_i + \lambda(x_k - x_i)$ 수식으로 설명드렸는데 쉽게 말씀드리면 결국 두 점 사이의 임의의 내분점을 의미합니다.

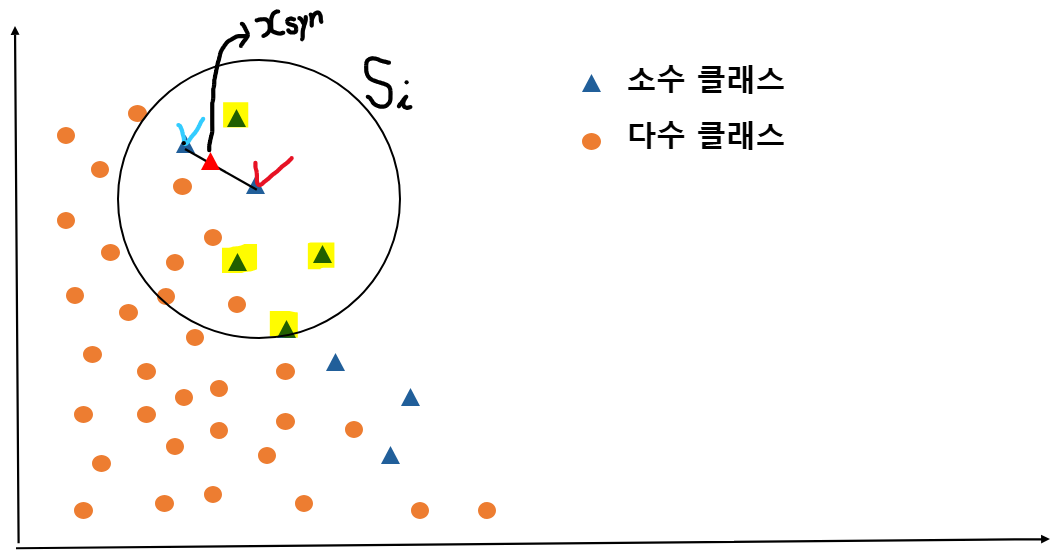
image-20240907143700099

4.$~$이 절차를 모든 삼각형 소수 클래스 데이터에 대해 반복적으로 실시합니다.

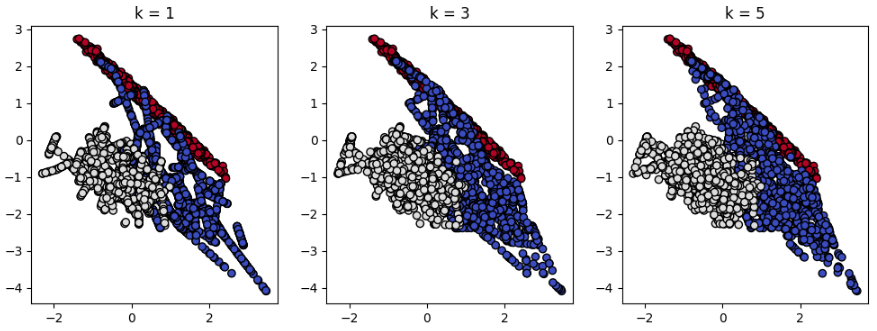
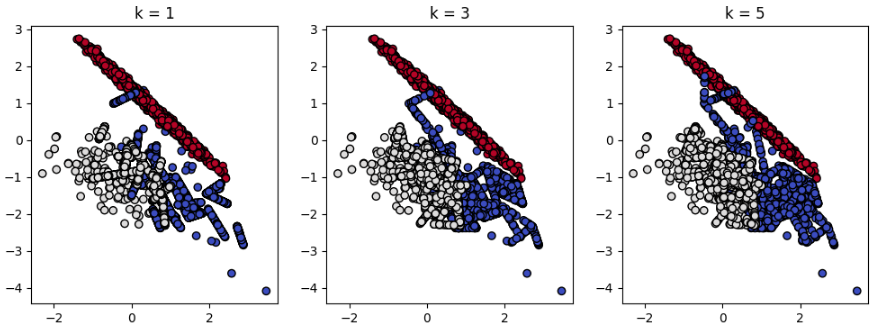
실제 데이터에 SMOTE를 적용해보겠습니다. 아래 그래프를 보면 k-nearest neighbors가 1일 때, 소수클래스인 파랑 점과 흰색 점들이 직선 형태로 OverSampling된 것을 볼 수 있습니다. 임의의 소수클래스 데이터 한 개와 가장 가까운 점 하나와의 내분점 형태로 새로운 점들이 반복적으로 생성되었기 때문에 직선 형태처럼 점들이 쭉 늘어선 것을 볼 수 있습니다. 즉, $k$가 늘어날수록 소수 클래스 데이터들 사이의 공백이 점점 사라지면서 새로운 데이터들이 채워지는 것을 볼 수 있습니다. 그래프의 우측 아래를 보면 확연하게 차이를 알 수 있습니다.

from imblearn.over_sampling import SMOTE

X, y = make_classification(n_classes = 3, weights = [0.03, 0.07, 0.9], n_features = 10,
                n_clusters_per_class = 1, n_samples = 2000, random_state = 10)
plt.figure(figsize = (12, 4))
k = [1, 3, 5]
for i in range(3) :
    j = i + 1
    plt.subplot(1, 3, j)
    sm = SMOTE(random_state = 1, k_neighbors = k[i])
    X_sm, y_sm = sm.fit_resample(X, y)
    plt.scatter(X_sm[:, 0], X_sm[:, 1], marker = 'o', c = y_sm,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
    plt.title('k = ' + str(k[i]))
    print('Resampled dataset shape %s' % Counter(y_sm))
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})

image-20240907150637831


3. Borderline-SMOTE

Borderline-SMOTE는 앞서 설명드린 SMOTE 기법과 거의 비슷합니다. 다만, 다수 클래스 데이터와 가까운 경계에 존재하는 소수 클래스 데이터만을 선택하여 SMOTE를 진행하는 기법을 말합니다. 모든 소수 클래스 데이터 각각에 대해서 가까운 다수 클래스 데이터가 얼마나 있느냐에 따라 3 분류로 나누게 됩니다. 즉, Noise, Danger, Safe로 나누게 됩니다. 이 중 Danger에 속한 소수 클래스만 SMOTE 기법을 사용하는 것이 Borderline-SMOTE 기법입니다. 절차는 다음과 같습니다.

  1. Borderline 정하기

    (1) 소수클래스 주변의 몇 개의 데이터를 K-nearest neighbors로 정할지, $k$값을 정합니다.

    (2) 소수클래스 데이터 중 하나인 관측치 $x_i$에 대해 K-nearest neighbors 셋을 생성합니다.

              단, K-nearest neighbors는 다수이든 소수이든 관계없습니다. -> 이 부분이 SMOTE와 조금 다릅니다.

         (3) K-nearest neighbors 셋 안에서

             - 모든 $k$개의 이웃들이 다수 클래스일 경우 : Noise

             - $k/2$개 초과 $k$개 미만의 이웃들이 다수 클래스일 경우 : Danger

             - $k/2$개 이하의 이웃들이 다수 클래스일 경우 : Safe

     2. Danger 소수 클래스 데이터만 앞서 설명드렸던 SMOTE 기법을 진행합니다.

        -> 이 때, K-nearest neighbors는 다시 소수클래스 데이터로만 뽑습니다.

쉽게 말해서, Borderline을 정하기 위한 K-nearest neighbors는 모든 데이터를 이웃으로 뽑고, Danger 소수 클래스 데이터에 대해 SMOTE를 진행할 때는 기존과 같이 소수클래스 데이터로만 K-nearest neighbors를 뽑습니다. 역시 그림으로 다시 설명드립니다.

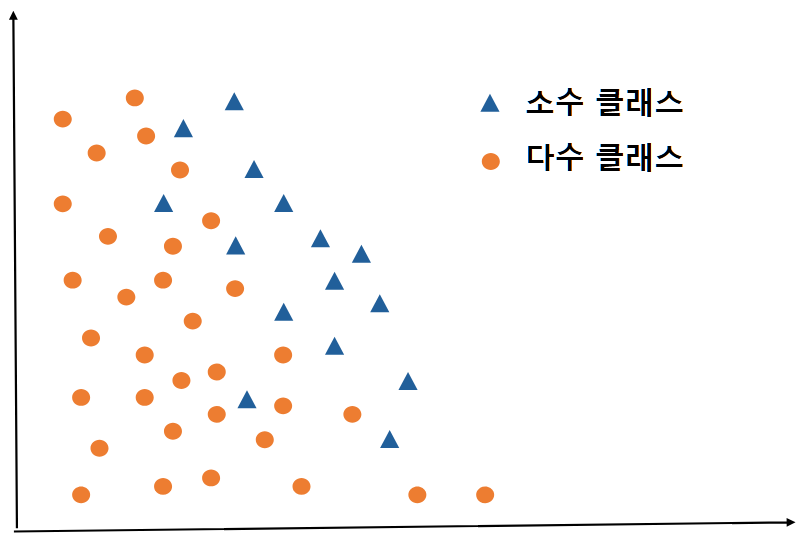
image-20240907160738806

1-(1). K-nearest neighbors $k$값 정하기 : $k$ 값은 $5$로 정해보겠습니다.

1-(2), (3). 모든 소수 클래스 데이터에 대해 K-nearest neighbors 셋을 구하고, Danger 소수 클래스를 찾습니다.

Safe의 경우, 소수 클래스쪽에만 있으므로 굳이 과대표집을 하더라도 유의미한 데이터가 아니기 때문에 OverSampling이 불필요하며, Noise의 경우 주변에 소수 클래스가 전혀 없으므로, 이상치인 Noise로 판단하여 과대표집하지 않습니다. 즉, 그림에서 Noise와 Safe 소수 클래스 데이터는 OverSampling하지 않습니다. 다만, 위쪽의 소수 클래스 데이터를 보면 주황 동그라미 데이터가 3개, 파랑 세모 데이터가 2개로 Danger에 해당됩니다. 이 데이터는 SMOTE를 진행하여 OverSampling을 진행합니다.

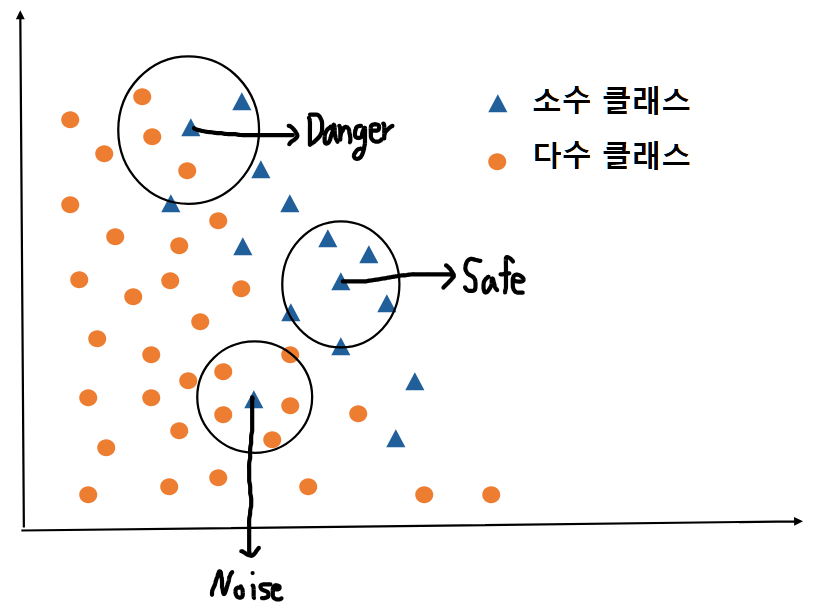
image-20240907160907008

2.  Danger 소수 클래스 데이터만 앞서 설명드렸던 SMOTE를 적용합니다.

아래와 같이 소수 클래스 데이터에 대해서만 다시 k-nearest neighbor를 구하면서 SMOTE를 진행할 것입니다.

image-20240907161621397

실제 데이터에 Borderline-SMOTE를 적용했을 때, SMOTE와 다른 결과가 나온 것을 볼 수 있습니다. 우측 아래를 보면 소수 클래스 데이터가 거의 생성되지 않은 것을 볼 수 있습니다. 즉, 다수 클래스와의 Borderline 부근에만 OverSampling이 발생한 것을 확인할 수 있습니다.

from imblearn.over_sampling import BorderlineSMOTE

X, y = make_classification(n_classes = 3, weights = [0.03, 0.07, 0.9], n_features = 10,
                n_clusters_per_class = 1, n_samples = 2000, random_state = 10)
plt.figure(figsize = (12, 4))
k = [1, 3, 5]
for i in range(3) :
    j = i + 1
    plt.subplot(1, 3, j)
    bsm = BorderlineSMOTE(random_state = 1, k_neighbors = k[i])
    X_bsm, y_bsm = bsm.fit_resample(X, y)
    plt.scatter(X_bsm[:, 0], X_bsm[:, 1], marker = 'o', c = y_bsm,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
    plt.title('k = ' + str(k[i]))
    print('Resampled dataset shape %s' % Counter(y_bsm))
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})
Resampled dataset shape Counter({2: 1795, 1: 1795, 0: 1795})

image-20240907162149140


4. ADASYN

ADASYN은 조절합성표집법(Adaptive Synthetic Sampling Method)을 의미하며 역시 SMOTE와 근본적으로는 같은 기법입니다. 다만, Sampling을 소수 클래스 데이터 위치에 따라 다르게 추출한다는 점이 다릅니다. 간단히 설명드리면, 각 소수 클래스 데이터마다 클래스 관계없이 K-nearest neighbor를 구했을 때, 다수 클래스가 이웃으로 포함되는 비율이 다를 것입니다. 소수 클래스 데이터마다의 그 비율들을 모두 구해서 가중치로 만들고, 이를 반영하여 OverSampling할 개수들을 분배합니다. 즉, 소수 클래스 데이터마다 추출되는 OverSampling 개수가 다르게 되는 것이죠. 역시 그림으로 설명드립니다.

1. K-nearest neighbors $k$값 정하기 : $k$ 값은 $5$로 정해보겠습니다.

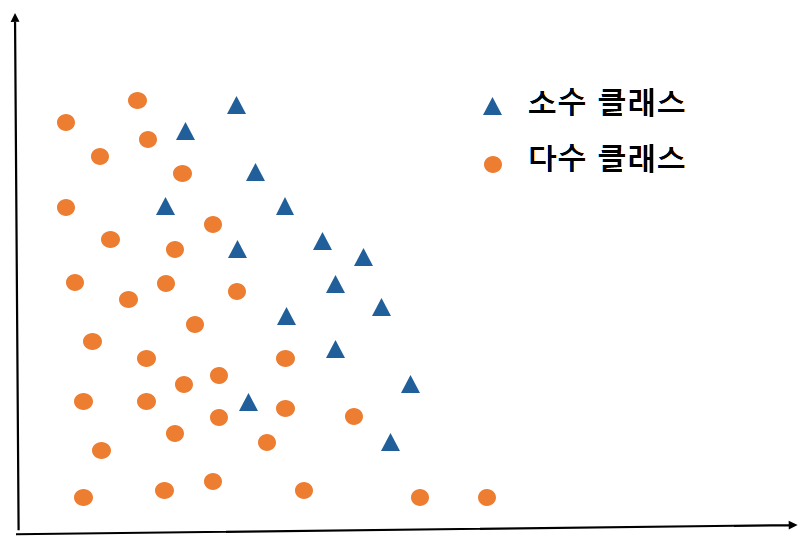
image-20240907164356768

2.  모든 소수 클래스 데이터에 대해 클래스와 관계없이 K-nearest neighbors를 구하고, 각각의 다수 클래스 이웃 비율을 구합니다.

     예를 들어, $r_1$은 $0.6$, $r_2$은 $0$, $r_3$은 $1$이 됩니다. 이를 모두 취합해서 오른쪽 표와 같이 정리합니다.

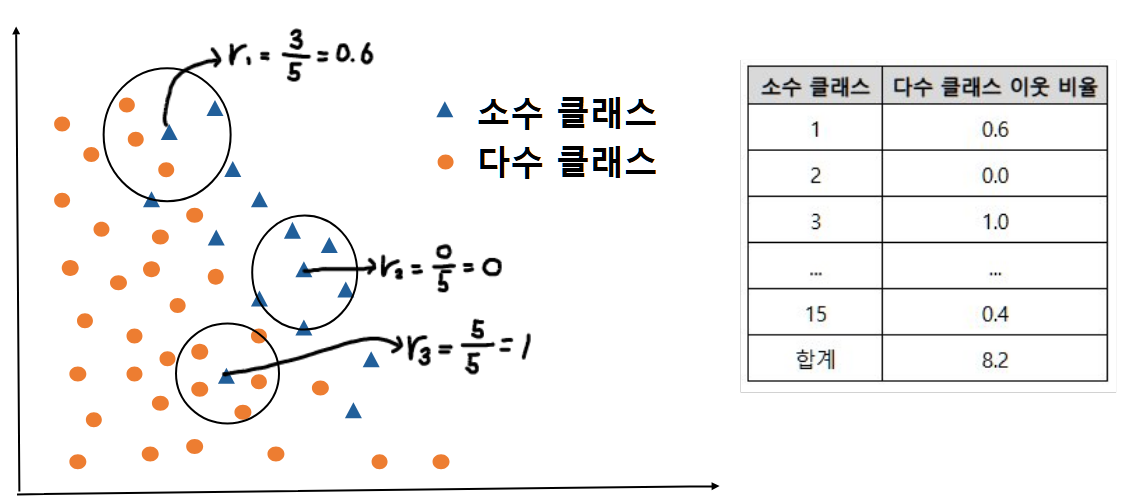
image-20240907170915668

3. 다수 클래스 이웃 비율의 합계가 $1$이 되도록 가중치를 곱합니다. 즉, 아래 표에서는 각 비율을 $8.2$로 나눕니다.

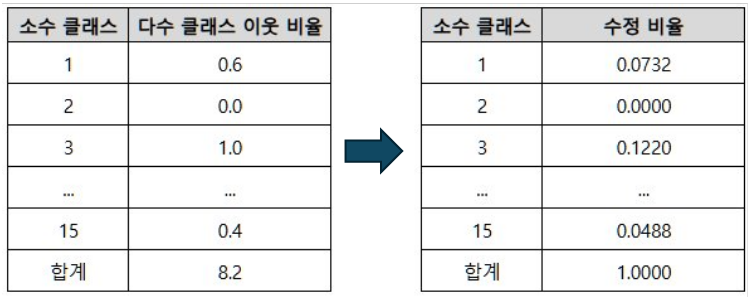
image-20240907171037487

4. OverSampling할 수량을 곱해서 각 소수 클래스마다 그 수량만큼 SMOTE를 이용해 생성합니다.

일반적으로 OverSampling할 수량은 다수 클래스 수량에 소수 클래스 수량을 뺀 수입니다. 예를 들어, 100개를 과대표집한다고 했을 때 아래와 같은 수량이 나오게 됩니다.

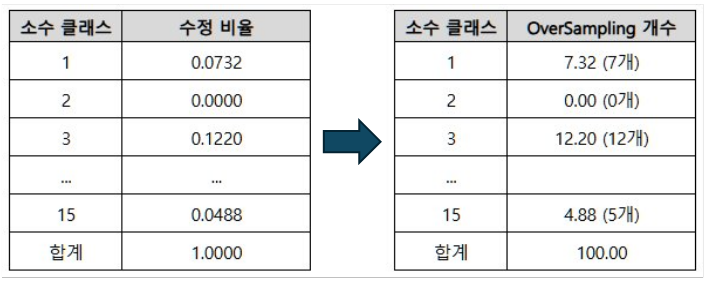
image-20240907171123495

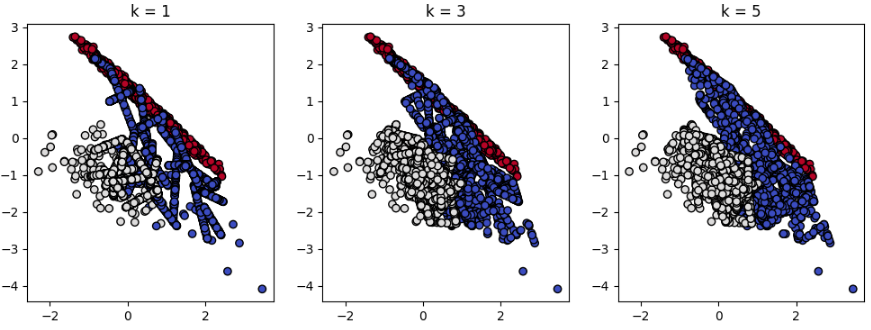
실제 데이터에 ADASYN을 적용해보았습니다. 역시 우측 아래를 보았을 때, SMOTE와 다르게 표집되지 않은 것을 볼 수 있습니다. 이는 다수클래스인 빨강 점들이 오른쪽 아래의 파랑 점들인 소수 클래스 K-nearest neighbors 셋에는 포함되지 않았기 때문으로 해석할 수 있습니다. 개수도 1795개가 아니라 약간 넘거나 부족한 것을 볼 수 있는데 개수가 소수로 나와 반올림한 개수가 존재하게 되서 합계가 맞지 않는 것을 볼 수 있습니다.

from imblearn.over_sampling import ADASYN

X, y = make_classification(n_classes = 3, weights = [0.03, 0.07, 0.9], n_features = 10,
                n_clusters_per_class = 1, n_samples = 2000, random_state = 10)
plt.figure(figsize = (12, 4))
k = [1, 3, 5]
for i in range(3) :
    j = i + 1
    plt.subplot(1, 3, j)
    ads = ADASYN(random_state = 1, n_neighbors = k[i])
    X_ads, y_ads = ads.fit_resample(X, y)
    plt.scatter(X_ads[:, 0], X_ads[:, 1], marker = 'o', c = y_ads,
               edgecolor = 'k', cmap = plt.cm.coolwarm)
    plt.title('k = ' + str(k[i]))
    print('Resampled dataset shape %s' % Counter(y_ads))
plt.show()
--------------------------------------------------------------------------------------------------------------------------------
Resampled dataset shape Counter({0: 1800, 2: 1795, 1: 1792})
Resampled dataset shape Counter({0: 1796, 2: 1795, 1: 1788})
Resampled dataset shape Counter({1: 1805, 2: 1795, 0: 1795})

image-20240907172123001

다음 포스팅에는 Sampling의 마지막인 Mixed Sampling에 대해 정리하도록 하겠습니다.


Reference

  1. 김성범[교수/산업경영공학부]
  2. cjkangme.log
  3. 파이썬을 이용한 통계적 머신러닝    [박유성 지음]
  4. minoue-xx
  5. cleansky.log
  6. Feel's blog


DATA_100%_LOGO_LIGHT



댓글남기기

참고

[연속형 분포] 코시 분포

안녕하세요! 최근 AI 기법들에 대해 설명 드렸었는데 잠시 쉬어가는 의미로 오랜만에 수리통계학 분포 시리즈로 돌아왔습니다. 올해 마지막 포스팅으로 코시 분포에 대해 설명드리도록 하겠습니다.

[Anomaly Detection] Isolation Forest

안녕하세요! 이번 시간에도 지난 포스트에 이은 Anomaly Detection 포스트입니다. 모델 기반 Anomaly Detection 기법 중 하나인 Isolation Forest에 대해 알아보도록 하겠습니다. 언뜻보면 Random Forest와 비슷한 부분도 있지만, 목적은...

[Anomaly Detection] LOF

이번 시간부터는 드디어 Anomaly Detection으로 넘어가보도록 하겠습니다. 평소에 이상탐지에 관심이 많았는데 재밌고 새로운 사실도 알게되서 너무 좋네요! 😄 Anomaly Detection 파트의 첫 번째 시간이기 때문에 간단히 이상탐지에 대해 알아보고, 밀도 기반 이...

[Sampling] Mixed sampling

이번 시간에는 Sampling의 마지막 포스트인 Mixed Sampling에 대해 알아보겠습니다. 즉, 앞서 설명드린 UnderSampling과 OverSampling을 모두 이용하는 Sampling 기법입니다. 간단히 2가지 정도를 소개하고 Sampling Chapter를 마...