이번 시간부터는 드디어 Anomaly Detection으로 넘어가보도록 하겠습니다. 평소에 이상탐지에 관심이 많았는데 재밌고 새로운 사실도 알게되서 너무 좋네요! 😄 Anomaly Detection 파트의 첫 번째 시간이기 때문에 간단히 이상탐지에 대해 알아보고, 밀도 기반 이상탐지 알고리즘인 LOF에 대해 설명드리도록 하겠습니다. LOF 모델의 장점과 한계점, 실제 예제 데이터를 이용한 실습 코드와 시각화까지 모두 정리해보도록 하겠습니다.

개요

1. 이상치란?

이상치의 사전적 의미는 대부분의 관측값과 크게 다른 데이터값을 의미합니다. 영어로 Novelty, Anomaly, Outlier 등으로 불리는데 각각 의미하는 바가 조금씩 다릅니다. 하지만 모두 이상치를 의미합니다! 아래 이미지와 같이 파랑색의 정상 관측값들과 달리 오른쪽 아래의 빨간 관측값처럼 다른 유형, 특성값을 가지는 것이 이상치라고 말씀드릴 수 있습니다.

Term Mean Example
Novelty 대부분의 데이터와 본질적인 특성은 같지만 유형이 다른 관측치 (긍정적인 의미) 호랑이가 정상일 때, 백호
Anomaly 대부분의 데이터와 다른 관측치 (부정적인 의미) 호랑이가 정상일 때, 라이거
Outlier 대부분의 데이터와 본질적으로 특성이 다른 관측치 (아주 부정적인 의미) 호랑이가 정상일 때, 사자 or 개구리

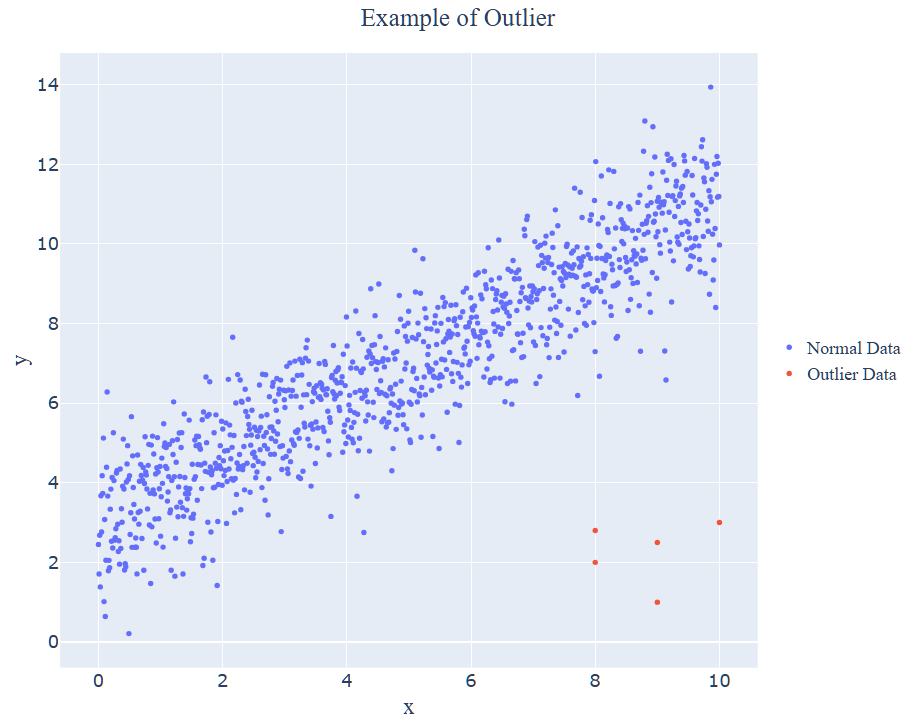
image-20241110092642098


2. 이상탐지 알고리즘이 필요한 이유

그렇다면 일반적인 분류 모델링을 사용하면 이상치를 분류할 수 있지 않을까요? 하지만 그리 쉽지 않습니다. 일반적으로 이상탐지를 해야 할 경우의 데이터는 다수의 정상 데이터와 소수의 이상치 데이터로 구성되어 있습니다. 즉, 심한 불균형 상태이며 지난 Sampling 포스트에서도 설명드렸듯이 이상치 데이터가 너무 적기 때문에 일반적인 머신러닝 모델로는 좋은 성능의 모델이 만들어지지 않습니다. SMOTE와 ADASYN과 같이 OverSampling 기법을 이용하는 방법도 있지만, 경험상 이상치 데이터가 10% 미만일 경우에는 과대표집으로 만들어지는 인공적인 데이터가 훨씬 많아지기 때문에 오히려 분산도 커지고 과대적합이 발생하여 모델의 예측력이 떨어집니다. 앞서 설명드린 기법들은 모두 지도학습이라 불리는 Supervised Learning 기법으로 종속변수 Y가 포함된 데이터를 예측하는 기법들입니다. 다만, 지도학습으로는 이상치 데이터를 올바르게 구분하기 어렵습니다.

그렇다면 어떤 방식으로 이상치를 분류해야 할까요? 바로 Unsupervised Learning을 적용해야 합니다. 종속변수 Y가 포함되지 않은 데이터를 이용하는데 모델 학습을 정상 데이터로만 Train을 시키고, Test 데이터를 적용했을 때 정상으로 판정되는 Boundary 바깥에 있으면 이상치로 판단을 내리는 방식으로 분류할 수 있습니다. 오로지 정상 데이터로만 학습을 시킨다는 점 때문에 이상치 탐지 알고리즘은 One-class Classification이라고도 부릅니다.


3. 이상탐지 알고리즘의 종류

이상탐지 알고리즘은 아래와 같이 크게 4가지로 나눌 수 있습니다.

  • 밀도 기반 Anomaly Detection : Gaussian Density Estimation, LOF 등
  • 모델 기반 Anomaly Detection : Isolation Forest, One-class SVM, SVD 등
  • 재구축 오차 기반 Anomaly Detection : PCA, AutoEncoder 등
  • 생성적 적대 신경망 기반 Anomaly Detection : AnoGAN, GANomaly 등

이 중 오늘 설명드릴 LOF 기법은 정상 데이터로부터 추정된 밀도를 기반으로 각 객체의 정상/이상을 판단하는 알고리즘인 밀도 기반 Anomaly Detection입니다.


4. LOF(Local Of Factor)

LOF(Local Of Factor)는 한 객체의 주변 데이터 밀도를 고려한 Anomaly Detection 기법입니다. 아래 이미지를 다시 살펴보았을 때, 하나의 파랑 점 정상 데이터 주변에 다른 데이터들도 빼곡하게 많이 붙어있는 것을 볼 수 있습니다. 이에 반해 빨강 점의 이상 데이터는 주변 데이터들이 거의 존재하지 않고, 단독으로 하나만 존재하고 있는 것을 볼 수 있습니다. 이와 같이 LOF는 하나의 데이터 주변의 데이터 밀도를 고려하여 이상치를 판별합니다.

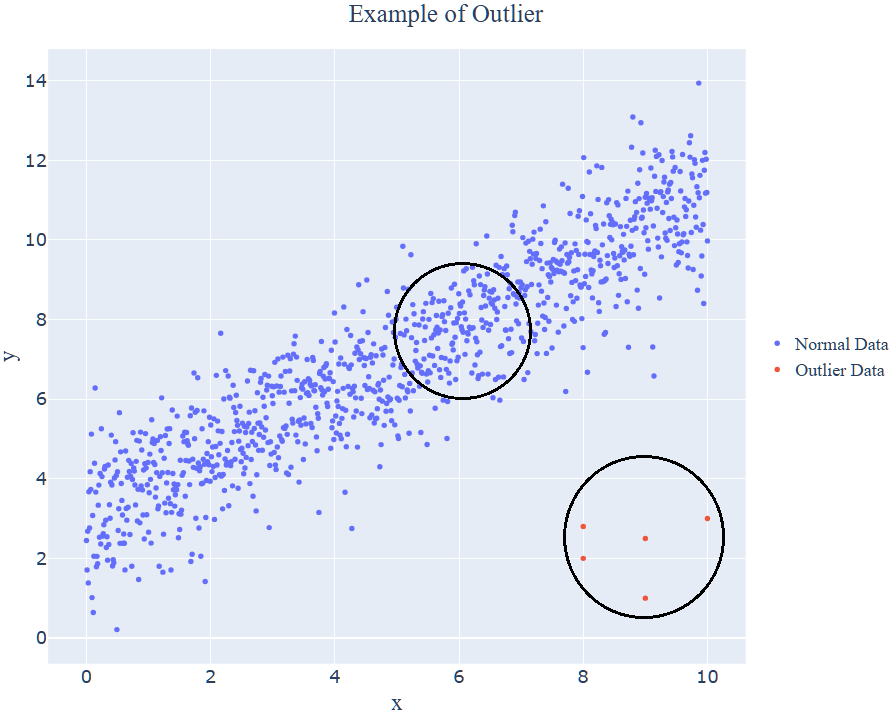
image-20241110163801676

LOF 기법은 각 데이터마다 Anomaly Score가 산출되고, Score 값이 커질수록 이상치임을 나타냅니다. 이 값이 어떻게 산출되는지 알아보겠습니다.

(1) k-distance of object $p$ : 자기 자신($p$)을 제외하고 $k$번째로 가까운 이웃과의 거리

예를 들어, 아래 사진에서 $k=4$라면, $4$-distance of object $p$는 $5$가 됩니다.

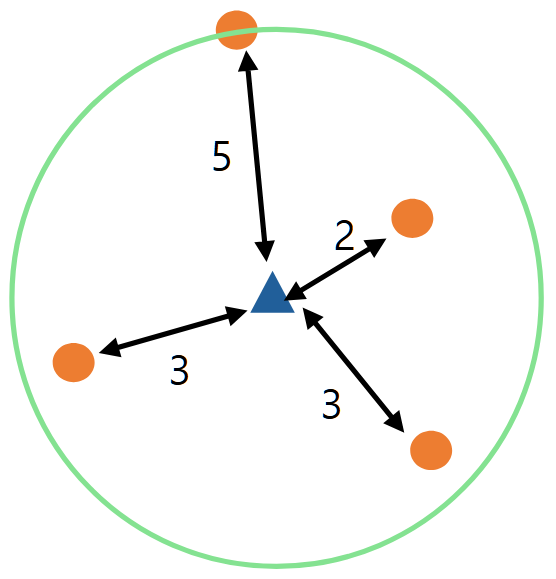
image-20241110170116845

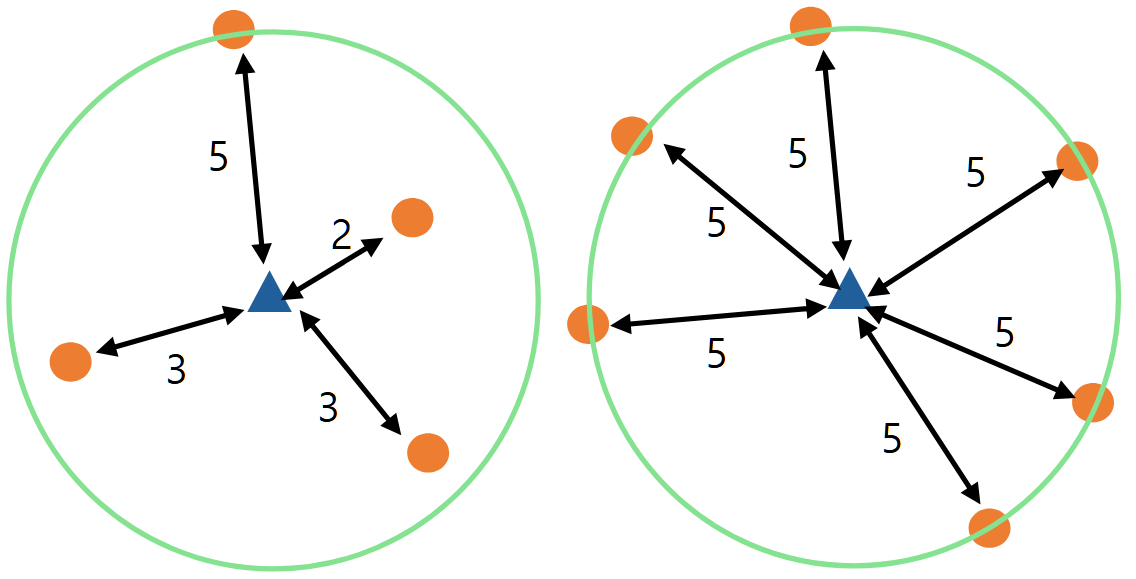
(2) k-distance neighborhood of object $p$ ; $N_{k}(p)$ : $k$번째로 가까운 이웃과의 거리를 원으로 표현할 때, 원 안에 포함되는 모든 객체들의 개수

언뜻 보면 $N_{k}(p)$는 $k$와 같은 값이 아닌가 생각할 수 있지만 다른 값입니다. 아래 이미지에서 왼쪽 예시는 $N_{4}(p) = 4$가 됩니다. 하지만 오른쪽 예시에서는 $N_{4}(p) = 6$이 되는 것을 알 수 있습니다. 즉, $k$와는 다른 값입니다.

image-20241110180132286

(3) Reachability Distance ; Reachability Distance$_{k}(p, o)$ : $o$를 기준으로 $k$번째 가까운 이웃과의 거리(k-distance of $o$)와 $o$, $p$ 사이 거리 간의 최대 값 ($=max${k-distance of $o$, $d(p, o)$})

이 부분부터는 조금 헷갈릴 수 있으니 잘 보셔야 합니다. Reachability Distance는 두 값 중 큰 값이 되는데, 그 두 값은 특정 데이터 $o$를 기준으로 $k$번째 가까운 이웃과의 거리와 $o$와 $p$ 사이 거리입니다. 유심히 봐야할 점은 데이터 $k$가 아닌 특정 데이터 $o$에 대한 k-distance 값이라는 점입니다. 이 점을 유념해서 예시를 들어보겠습니다.

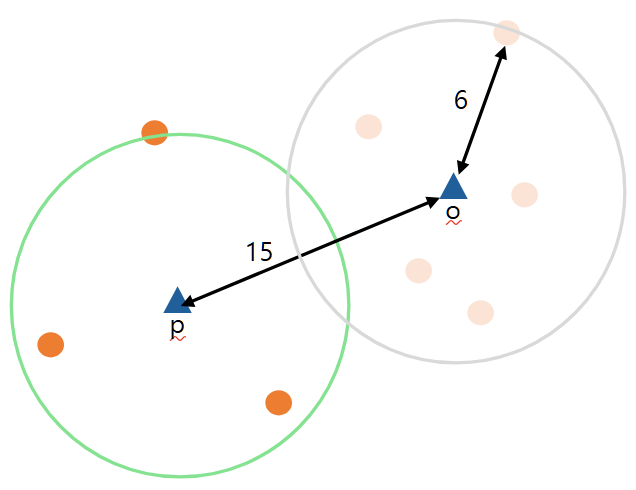
아래와 같이 점 $o$와 점 $p$가 있을 때, Reachability Distance$_{5}(p, o)$는 $max${5-distance of $o$, $d(p, o)$}$=max${$6$, $15$}$=15$가 되는 것을 알 수 있습니다.

image-20241110190357395

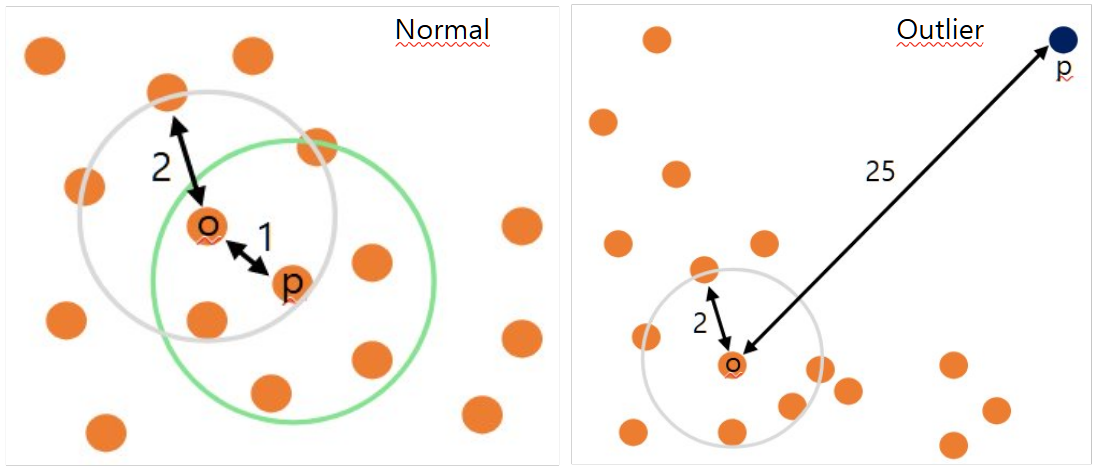
Reachability Distance가 시사하는 바에 대해 알아보겠습니다. 왼쪽 이미지와 같이 정상 데이터에서는 주변에도 데이터들이 모여있기 때문에 Reachability Distance$_{5}(p, o)=2$가 됩니다. 그러나 오른쪽과 같이 Outlier 데이터에서는 Reachability Distance$_{5}(p, o)=25$가 됩니다. 즉, Reachability Distance가 클수록 이상치가 될 가능성이 크다는 것을 의미합니다.

image-20241110192416833

(4) Local reachability density of object $p$ ; $Ird_{k}(p)$ : 여러 reachability distance를 하나의 지표로 계산한 값

$Ird_{k}(p)$는 아래와 같이 정의하며, (3)에서 특정짓지 않았던 점 $o$도 $N_{k}(p)$에 속하는 점들로 정의합니다.

$ \begin{align*} Ird_{k}(p) = \frac { |N_{k}(p)| }{ \sum_{o \in N_{k}(p)} \rm{reachability~distance}_{k}(p, o) } \\ \end{align*} $

즉, $Ird_{k}(p)$의 분모는 $N_{k}(p)$에 속하는 모든 점들 $o$에 대한 reachability distance의 합으로 정의됩니다. 따라서, (3)과는 반대로 정상 데이터일 경우, reachability distance의 합이 작아질 것이기 때문에 $Ird_{k}(p)$ 값이 커질 것이며, 이상 데이터일 경우 $Ird_{k}(p)$ 값은 작아집니다.

(5) Local Outlier Factor of object $p$ ; $LOF_{k}(p)$

최종적인 LOF 기법의 Anomaly Score 값입니다.

$ \begin{align*} Ird_{k}(p) = \frac { \sum_{o \in N_{k}(p)} Ird_{k}(o) / Ird_{k}(p) }{ |N_{k}(p)| } \\ \end{align*} $

각각 Case 별로 살펴보도록 하겠습니다. 그 전에 하나만 기억하면 됩니다. $p$가 정상 데이터일수록 주변 밀도는 높아지고 $Ird\_{k}(p)$의 값은 커진다!

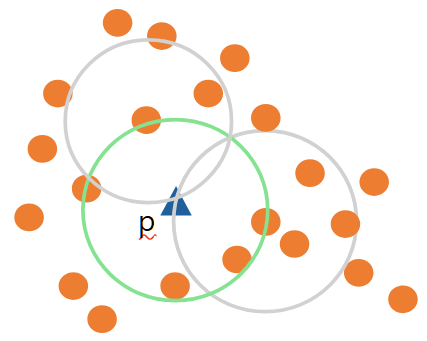
  • 데이터 $p$ 주변 밀도가 높은 경우
    • 설명드렸듯이, 주변 밀도가 높아지면 $Ird_{k}(p)$은 커집니다. 그리고 주변에 있던 데이터 $o$의 주변 밀도도 클 것이므로 $Ird_{k}(o)$도 커집니다. 즉, $LOF_{k}(p)$는 $1$에 가까운 값을 가지게 될 것입니다.

image-20241110202015179

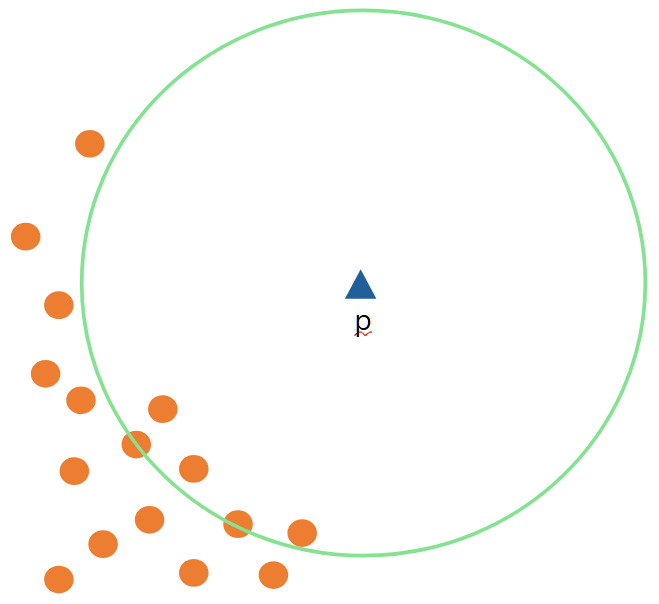
  • 데이터 $p$ 주변 밀도가 낮은데 데이터 $o$ 주변 밀도는 큰 경우

    • $Ird_{k}(p)$ 값은 작을 것이며, $Ird_{k}(o)$ 값은 클 것입니다. 따라서 $LOF_{k}(p)$는 $1$보다 상당히 큰 값을 가질 것이며, 데이터 $p$는 이상치일 가능성이 높습니다.

      image-20241110202550894

  • 데이터 $p$ 와 데이터 $o$ 주변 밀도가 모두 낮은 경우

    • 주변 밀도가 모두 낮으므로 $Ird_{k}(p)$ 값과 $Ird_{k}(o)$ 값 모두 작을 것이며, $LOF_{k}(p)$는 $1$에 가까운 값을 가질 것입니다.

image-20241110203123065

Case $LOF_{k}(p)$ Outcome
데이터 $p$ 주변 밀도가 높은 경우 $1$에 가까운 값 Normal
데이터 $p$ 주변 밀도가 낮은데 데이터 $o$ 주변 밀도는 큰 경우 $1$보다 상당히 큰 값 Outlier
데이터 $p$ 와 데이터 $o$ 주변 밀도가 모두 낮은 경우 $1$에 가까운 값 Normal

아래는 위키독스에 있는 예시로, 각 데이터마다의 LOF Anomaly Score를 기입한 그래프입니다. 보시다시피 주변 밀도가 높은 정상 데이터들은 점수가 1 근방인 반면, 혼자 단독으로 떨어져있는 Outlier의 경우 1보다 큰 3~7 사이의 값을 가지는 것을 알 수 있습니다.

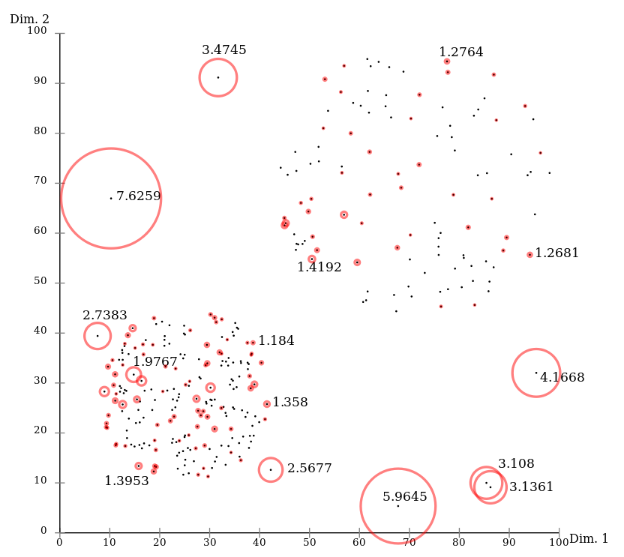
image-20241110203926580


5. LOF의 한계점

LOF 기법은 단순하면서도 생각보다 Powerful한 성능을 내는 기법입니다. 하지만 한계점도 명확하게 존재하는데 가장 큰 문제는 사용자에 따라 결과가 달라질 수 있다는 점입니다. 예를 들어, LOF Anomaly Score는 제한 없이 무한대까지 점수를 얻을 수 있지만, 얼마나 점수가 커야 Outlier로 정할지 기준이 없습니다. 즉, Outlier 기준을 임의로 정해야 하고, $k$ 값도 사용자가 정해야 하기 때문에 사용자에 따라 Outlier 판별 결과가 달라질 수 있습니다. 일반적으로 이상치 개수를 전체 데이터 중 몇 %로 할지 정하는 방식으로 LOF를 사용합니다.

또한, KNN을 사용하기 때문에 계산복잡도가 상당히 크며 고차원의 데이터이면 잘 맞지 않다는 점도 한계점으로 볼 수 있습니다.


실습

실습을 진행해보도록 하겠습니다. 데이터는 인공적으로 제가 만든 데이터이며, 1000개의 정상 데이터와 10개의 이상 데이터를 구성하여 LOF 기법을 적용해 보았습니다.

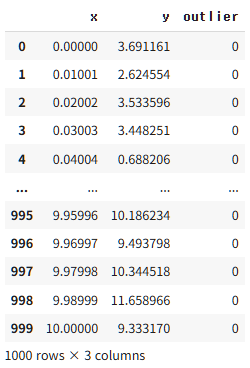
먼저 정상 데이터는 $y = a + bx + e$에 따라 선형성의 그래프가 그려지도록 생성했습니다. 여기서 $e$는 정규분포 난수를 의미합니다.

import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go

x = np.linspace(0, 10, 1000)

a = 3
b = 0.8
e = np.random.normal(size = 1000)

y = a + b * x + e

data1 = pd.DataFrame({"x" : x, "y" : y, "outlier" : 0})
data1

image-20241110225733914

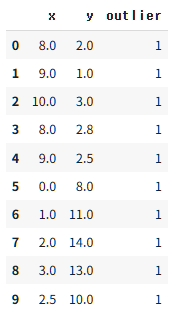
다음으로 이상 데이터는 임의로 10개를 생성하여 아래와 같이 구성하여 정상데이터와 합칩니다.

data2 = pd.DataFrame({"x" : [8, 9, 10, 8, 9, 0, 1, 2, 3, 2.5], "y" : [2, 1, 3, 2.8, 2.5, 8, 11, 14, 13, 10], "outlier" : 1})
data2

image-20241110230208976

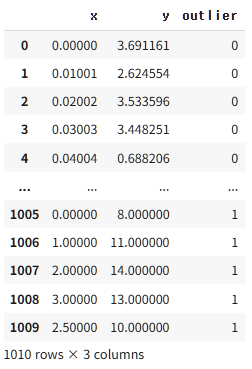
data3 = pd.concat([data1, data2], axis = 0).reset_index(drop = True)
data3

image-20241110230303651

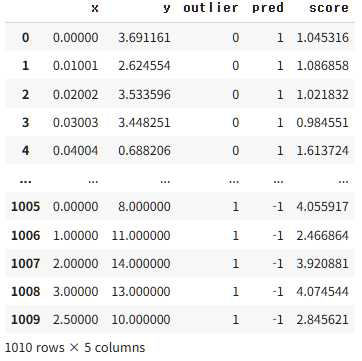
LOF 기법은 sklearn.neighbors 내 LocalOutlierFactor 함수를 통해 적용할 수 있습니다. $k=7$로 지정하고, Outlier 판정 비율을 의미하는 $\rm{contamination}=0.01$로 지정하여 분석했습니다. 따라서 1010개의 데이터 중 11개를 Outlier로 예측했고, Outlier의 값들의 Anomaly Score가 2 이상의 큰 값을 가지는 것을 확인할 수 있습니다.

from sklearn.neighbors import LocalOutlierFactor

X = data3.drop(['outlier'], axis = 1)
y = data3['outlier']
data4 = data3.copy()

outlier = LocalOutlierFactor(n_neighbors = 7, contamination = 0.01)     # contamination : 몇 프로 정도를 outlier로 정할거냐
y_predict = outlier.fit_predict(X)
data4['pred'] = y_predict

print(data4.value_counts(['pred']))
data4['score'] = -outlier.negative_outlier_factor_
data4
--------------------------------------------------------------------------------------------------------------------------------
pred
 1      999
-1       11
Name: count, dtype: int64

image-20241110230720552

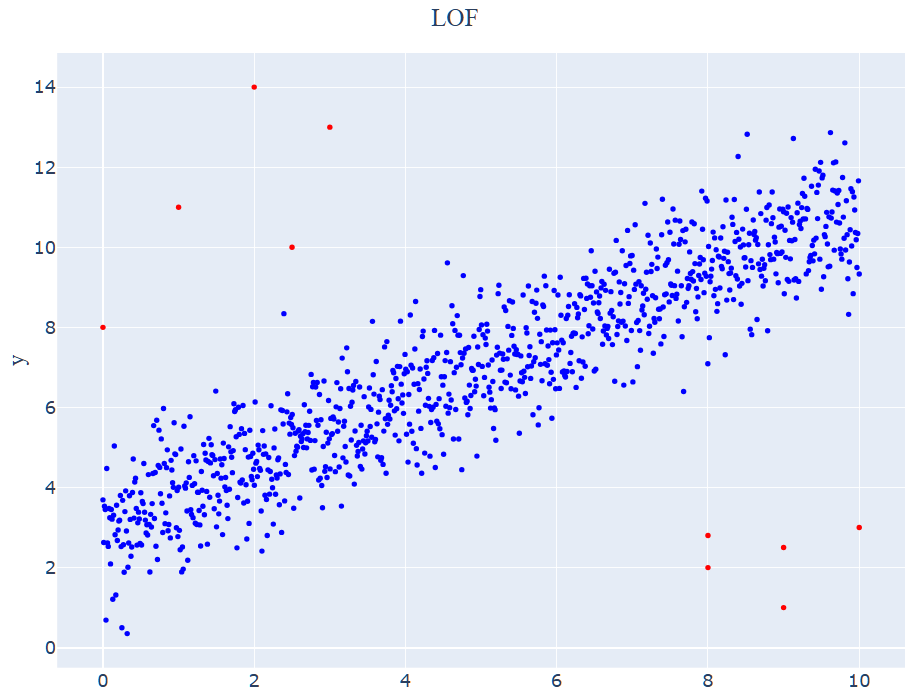
아래 그래프에서 파랑 점들은 실제 정상 데이터, 빨강 점들이 실제 이상치 데이터를 나타냅니다.

fig = go.Figure()
fig.add_trace(go.Scatter(x = data4['x'], y = data4['y'], name = 'LOF', mode = "markers", marker_color = data4['outlier'], marker_colorscale = "Bluered"))
my_font = 'Times New Roman'
fig.update_layout(legend = dict(y = 0.5, font_size = 20, font_family = my_font), title = "LOF", title_font_family = my_font, font_size = 20, title_x = 0.5)
fig.update_layout(margin = dict(l = 0, r = 0, t = 60, b = 0), width = 1000, height = 800)
fig.update_xaxes(title_text = 'x', title_font_family = my_font)
fig.update_yaxes(title_text = 'y', title_font_family = my_font)
fig.show()

image-20241110230917688

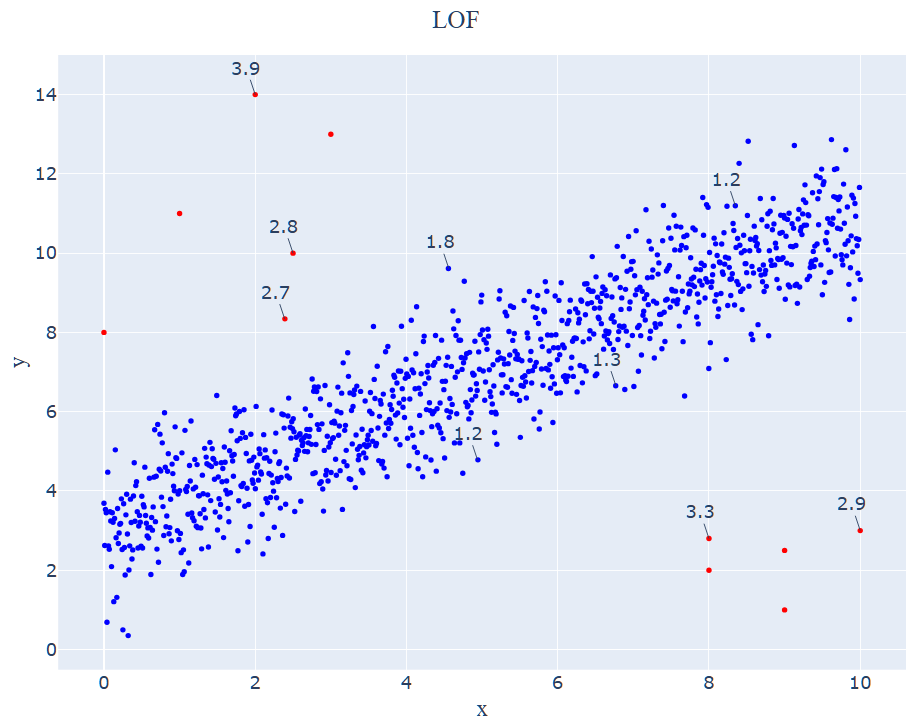
아래 그래프는 LOF를 통해 예측한 결과로, 실제 이상치 값들에 더하여 정상 데이터 1개까지 11개를 Outlier로 예측하고 있습니다. 일부 데이터들의 Anomaly Score 값들을 Annotation 해주었는데, 보시다시피 Outlier라고 예측한 빨강 점들의 Score 값이 2 이상으로 큰 값을 가지는 것을 확인할 수 있습니다.

fig = go.Figure()
fig.add_trace(go.Scatter(x = data4['x'], y = data4['y'], name = 'LOF', mode = "markers", marker_color = data4['pred'], marker_colorscale = "Bluered_r",
                         text = data4['score']))
my_font = 'Times New Roman' # "Times New Roman", 'Arial'
fig.update_layout(legend = dict(y = 0.5, font_size = 20, font_family = my_font), title = "LOF", title_font_family = my_font, font_size = 20, title_x = 0.5)
fig.update_layout(margin = dict(l = 0, r = 0, t = 60, b = 0), width = 1000, height = 800)
fig.update_xaxes(title_text = 'x', title_font_family = my_font)
fig.update_yaxes(title_text = 'y', title_font_family = my_font)

fig.add_annotation(x = 8, y = 2.8, text = "3.3")
fig.add_annotation(x = 10, y = 3, text = "2.9")
fig.add_annotation(x = 2, y = 14, text = "3.9")
fig.add_annotation(x = 2.5, y = 10, text = "2.8")
fig.add_annotation(x = 2.39, y = 8.34, text = "2.7")
fig.add_annotation(x = 4.94, y = 4.78, text = "1.2")
fig.add_annotation(x = 4.56, y = 9.61, text = "1.8")
fig.add_annotation(x = 8.35, y = 11.19, text = "1.2")
fig.add_annotation(x = 6.77, y = 6.65, text = "1.3")

fig.show()

image-20241110231056702


Reference

  1. 김성범[교수/산업경영공학부]
  2. 김성범[교수/산업경영공학부]
  3. Fast Campus : 30개 사례로 배우는 Anomaly Detection 알고리즘 구현과 실전 프로젝트 Online
  4. Deep Learning Bible - D. Un-supervised Learning - Eng.


DATA_100%_LOGO_LIGHT



댓글남기기

참고

[연속형 분포] 코시 분포

안녕하세요! 최근 AI 기법들에 대해 설명 드렸었는데 잠시 쉬어가는 의미로 오랜만에 수리통계학 분포 시리즈로 돌아왔습니다. 올해 마지막 포스팅으로 코시 분포에 대해 설명드리도록 하겠습니다.

[Anomaly Detection] Isolation Forest

안녕하세요! 이번 시간에도 지난 포스트에 이은 Anomaly Detection 포스트입니다. 모델 기반 Anomaly Detection 기법 중 하나인 Isolation Forest에 대해 알아보도록 하겠습니다. 언뜻보면 Random Forest와 비슷한 부분도 있지만, 목적은...

[Sampling] Mixed sampling

이번 시간에는 Sampling의 마지막 포스트인 Mixed Sampling에 대해 알아보겠습니다. 즉, 앞서 설명드린 UnderSampling과 OverSampling을 모두 이용하는 Sampling 기법입니다. 간단히 2가지 정도를 소개하고 Sampling Chapter를 마...

[Sampling] Oversampling

안녕하세요. 지난 포스트인 UnderSampling에 이어서 Sampling 기법 중 하나인 OverSampling에 대해 알아보겠습니다. 일반적으로 머신러닝에서 UnderSampling보다 많이 사용되며, 4가지 정도 소개하도록 하겠습니다.