안녕하세요! 이번 시간에도 지난 포스트에 이은 Anomaly Detection 포스트입니다. 모델 기반 Anomaly Detection 기법 중 하나인 Isolation Forest에 대해 알아보도록 하겠습니다. 언뜻보면 Random Forest와 비슷한 부분도 있지만, 목적은 전혀 다릅니다. 의사결정나무에 대한 사전 지식이 있다면 이해하기 쉽고, 실제로 이상탐지 대회에서도 많이 사용하는 기법 중 하나입니다.

개요

1. Isolation Forest란?

머신러닝 앙상블 모델을 공부할 때, 가장 먼저 배우는 기법 중 하나가 Random Forest일 것입니다. Random Forest는 의사결정나무의 Bagging 버전이라고 보면 되는데, 쉽게 말해서 여러 개의 의사결정나무를 복원추출하여 각각의 나온 결과들을 앙상블하여 하나로 취합한 것이라고 생각하면 됩니다. 그리고 그 목적은 종속변수인 Y를 얼마나 잘 예측하냐가 될 것입니다.

모델 기반 Anomaly Detection 기법 중 하나인 Isolation Forest도 의사결정나무를 이용한다는 점에서 Random Forest와 비슷하지만, 정상 데이터로부터 학습한 모델을 기반으로 각 객체의 정상과 이상 여부를 판단하는 것을 목적으로 합니다. 또한, Random Forest는 Supervised Learning이므로 종속 변수 Y를 이용하지만, Isolation Forest는 Unsupervised Learning으로 종속 변수 Y를 이용하지 않습니다.


2. Concept

Isolation Forest는 하나의 데이터를 고립시키는 TREE 모델을 구축하는 이상탐지 기법입니다. 그렇다면 Isolation Forest는 어떻게 의사나무결정을 통해 이상치를 판단할 수 있는 것일까요? Concept은 아래 가정에서부터 시작합니다.

정상 관측치보다 이상 관측치를 고립시키는 것이 쉬울 것이다.

예시를 들어보도록 하겠습니다. 아래 파란 점은 정상 데이터입니다. 이 때, 가상의 TREE 모델이 파란 점을 고립시키기 위해 노드 분할을 실시합니다. 아무래도 정상 데이터는 주위에 밀집되어 있는 데이터들이 있으므로, 노드 분리 횟수가 6회로 많습니다.

(참고로, Isolation Forest는 모델 기반의 Anomaly Detection이지만, 위와 같이 밀도 기반의 Anomaly Detection 특징인 데이터 밀집도에 대한 개념도 일부 이용하는 기법입니다.)

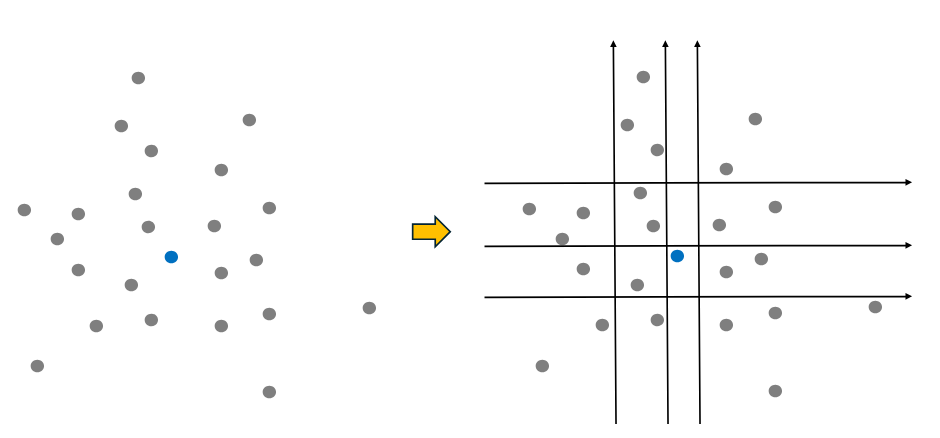
image-20241116222352923

빨강 점의 이상 데이터도 노드 분리 해보도록 하겠습니다. 보시다시피 이상치이기 때문에 노드 분리 횟수가 2회로 쉽게 분리되는 것을 볼 수 있습니다.

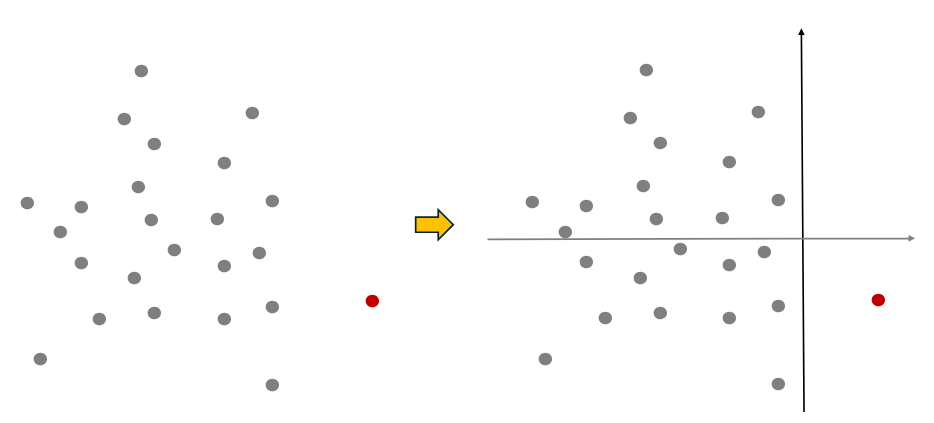
image-20241116222629644

즉, 이상 데이터의 노드 분리 횟수가 정상 데이터보다 일반적으로 적다는 점을 이용합니다. 결론적으로 특정 데이터를 고립시키기 위한 노드 분리 횟수(path length)를 이상치 점수인 Anomaly Score로 활용하면서 데이터를 정상/이상으로 분류하는 기법이 Isolation Forest의 Concept입니다.


3. 절차

절차 역시 Random Forest와 비슷한 부분이 많습니다. 전체 데이터가 아닌 일부 Sampling한 데이터만 TREE 모델에 적합시킵니다. 여기서 Sub-Sampling은 Random Forest와 같은 복원추출(Bagging)이 아닌 비복원추출(Pasting)이 default 값입니다. 물론 복원추출하도록 Parameter 변경도 가능합니다. (bootstrap = True)

그리고 Sampling한 데이터에 대해 임의의 변수와 임의의 분할점을 사용해서 조건을 만족할 때까지 이진분할을 진행합니다. 조건은 TREE 모델이 사전에 정한 Depth까지 도달, 모든 Terminal Node에 데이터가 1개씩만 존재 등이 될 수 있습니다.

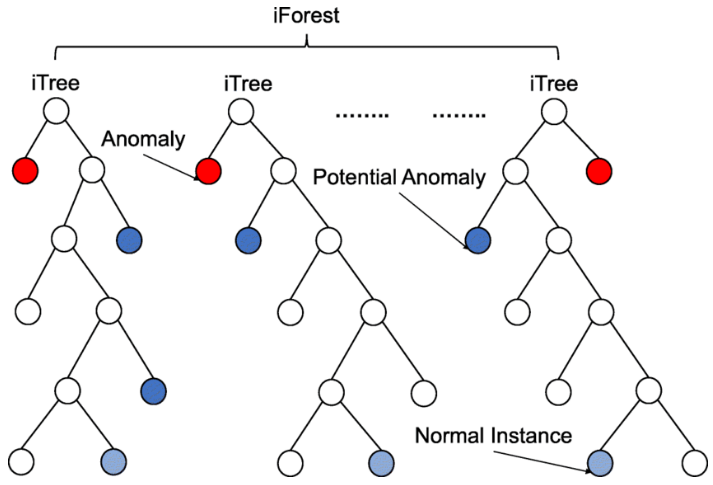
앞서 말씀드린 Concept을 아래 그림으로 살펴보면, 가장 먼저 분리된 빨간 데이터를 Outlier로, 두 번째 Depth에서 분리된 데이터를 잠재적 Outlier로 판단하고 있습니다. 가장 늦게 분리된 데이터는 정상 데이터로 예측합니다. 이와 같이 여러 개의 TREE를 만들고, 각각의 관측치마다 노드 분리 횟수(path length)를 통한 Anomaly Score를 저장하여 앙상블하면 Isolation Forest 모델 적합이 완료됩니다.

image-20241116221513060


4. Anomaly Score

그렇다면 Anomaly Score는 단순히 노드 분리 횟수(path length)를 의미하는 것일까요? 아닙니다. 노드 분리 횟수 자체를 Score로 만들면 0에서 무한대까지 점수가 나올 수 있기 때문입니다. 지난 포스트인 LOF에서도 무한대까지 점수가 만들어져 이상치에 대한 기준이 모호했었습니다. 이러한 문제를 해결하기 위해 아래와 같이 0과 1사이로 Scale한 노드 분리 횟수 기반의 Score가 만들어지게 됩니다.

$ \begin{align*} s(x, n) &= 2^{-\frac {E(h(x))}{c(n)}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ \end{align*} $
$ \begin{align*} c(n) &= 2H(n-1)- \frac {2(n-1)}{n}, \\ H(i) &= \rm{ln}(i) + 0.5772156649~~ (\rm{Euler's ~~ constant})) \\ \end{align*} $

  • $x$ : 특정 데이터
  • $n$ : 총 데이터 수 (=데이터 행 수)
  • $h(x)$ : 특정 데이터 $x$의 노드 분리 횟수(Path length)
  • $E[h(x)]$ : 각 TREE에 대한 $h(x)$의 평균
  • $c(n)$ : 모든 데이터들의 평균 노드 분리 횟수(Path length)를 의미하며, 일반적으로 위의 식 $c(n)$과 비슷한 값을 가진다고 합니다.
  • Euler’s constant : 0.5772156649를 의미하며, $h(x)$를 Normalize하기 위해 사용된 상수

각각 Normal Data와 Outlier일 때의 Anomaly Score는 어떻게 될까요? Anomaly Score가 $0$에 가까울 수록 정상 데이터, $1$에 가까울 수록 이상 데이터임을 나타냅니다.

  • 이상 데이터일 경우 : Path length의 평균값은 $0$에 가깝게 됩니다.
    • $E[h(x)] \rightarrow 0, ~~$$s(x, n)~$$ \rightarrow 2^0 \rightarrow$ $1$
  • 정상 데이터일 경우 : Path length의 평균값은 총 데이터 수에서 1을 뺀 $n-1$에 가깝게 됩니다.
    • $E[h(x)] \rightarrow (n-1), ~~$$s(x, n)~$$ \rightarrow 2^{-(n-1)} \rightarrow$ $0$
  • $E[h(x)] = c(n)$ : 특정 데이터의 Path length 값이 모든 데이터들의 평균 노드 분리 횟수와 비슷할 경우
    • $E[h(x)] \rightarrow c(n), ~~$$s(x, n)~$$ \rightarrow 2^{-1} \rightarrow$ $0.5$

5. 장단점

Isolation Forest의 우수한 성능은 익히 알려져 있는 만큼 실제 프로젝트에서도 많이 이용됩니다. 모든 데이터를 이용하지 않고 Sampling한 데이터를 TREE에 적합시키기 때문에 군집 기반 Anomaly Detection에 비해 계산량이 매우 적은 것도 하나의 장점입니다. 다만, 노드 분리 시 수직/수평으로만 데이터를 나누기 때문에 잘못된 Anomaly Score가 발생할 수 있습니다. 이를 해결하기 위해 Extended Isolation Forest (EIF)가 고안되었으며, 추후에 이에 대해 포스팅하도록 하겠습니다.


실습

이번 실습 데이터는 Kaggle의 Credit Card Fraud Detection을 사용해 보았습니다. 28만 개가 넘을 정도로 큰 데이터이기 때문에 앞의 3만 개만 끊어서 사용했고, 중복 데이터 제거 이외에 특별한 전처리를 하지 않은 상태에서 Isolation Forest를 적용해 보았습니다.

  • 데이터 특징
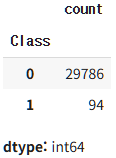
    • Shape : $(29880, 31)$
    • class : {Normal : 29786개, Outlier : 94개}

kagglehub를 통해 데이터를 불러옵니다. drop_duplicates()를 통해 중복 데이터를 제거하여 29,880개의 Dataset을 만들었습니다.

import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import kagglehub

path = kagglehub.dataset_download("mlg-ulb/creditcardfraud")
raw_data = pd.read_csv(path + "/creditcard.csv")
data = raw_data.loc[:30000, :].copy()
data = data.drop_duplicates()
print(data.shape)
data['Class'].value_counts()
--------------------------------------------------------------------------------------------------------------------------------
(29880, 31)

image-20241117212841625

여러 변수 중 ‘V3’와 ‘V4’를 선정하여 2차원 그래프를 그려보았습니다. 빨강 점들은 Outlier, 파랑 점들은 Normal Data를 의미합니다.

fig = go.Figure()
fig.add_trace(go.Scatter(x = data['V3'], y = data['V4'], mode = "markers", marker_color = data['Class'], marker_colorscale = "Bluered"))
my_font = 'Times New Roman'
fig.update_layout(legend = dict(y = 0.5, font_size = 20, font_family = my_font), title = 'Credit Card Fraud Detection', title_font_family = my_font, font_size = 20, title_x = 0.5)
fig.update_layout(margin = dict(l = 0, r = 0, t = 60, b = 0), width = 800, height = 600)
fig.update_xaxes(title_text = 'V3', title_font_family = my_font)
fig.update_yaxes(title_text = 'V4', title_font_family = my_font)

fig.show()

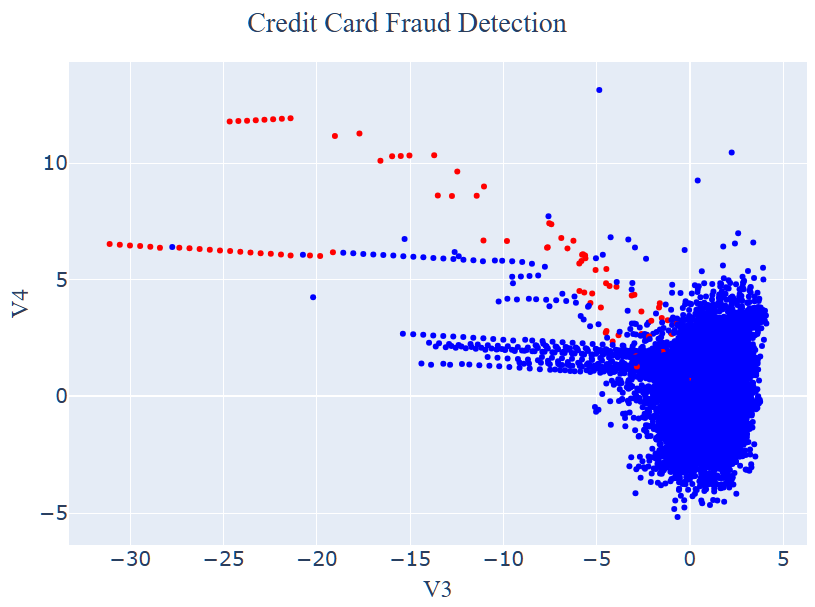
image-20241117213208163

데이터를 X와 y로 나눈 후, 94개의 Outlier Index 값을 살펴보았습니다.

X = data.drop('Class', axis = 1)
y = data.loc[:, 'Class':'Class']
X.reset_index(inplace = True, drop = True)
y.reset_index(inplace = True, drop = True)

y.loc[y['Class'] == 1, :]

image-20241117213433410

Isolation Forest는 sklearn.ensemble 내에 내장되어 있습니다. contamination은 Outlier 판정 비율을 의미하며, 실제 Outlier 비율인 0.0031로 지정했습니다. 이때, 정상 데이터의 Prediction 값은 $1$, Outlier는 $-1$로 도출됩니다.

또한, decision_function을 통해 Anomaly Score 값을 알 수 있습니다. 그런데 아래 값을 보면 $0 \sim 1$이 아닌 $-0.5 \sim 0.5$로 보정되어 있으며, 어째서인지 Outlier 일수록 음수에 가깝게 나오고 있습니다.

이는 Outlier 예측값이 $-1$로 나오기 때문에 Score 값도 이상치일수록 음수 값으로 나타나지도록 보정한 것 때문입니다. 따라서, Anomaly Score를 정확하게 알고 싶다면 $0.5$-IsF.decision_function()으로 해줘야 합니다.

from sklearn.ensemble import IsolationForest

IsF = IsolationForest(contamination = 0.0031, random_state = 39)
IsF.fit(X)
y_pred = IsF.predict(X)
y_pred2 = pd.DataFrame(y_pred, columns = ['y_pred'])
print(y_pred[27600 : 27650])
print(IsF.decision_function(X)[27600 : 27650])
--------------------------------------------------------------------------------------------------------------------------------
[ 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1  1  1  1  1
  1  1]
[ 0.29501318  0.25446702  0.26842696  0.28128502  0.25848993  0.1770815
  0.25838384  0.14001897  0.21512459  0.2041324   0.28940446  0.28336387
  0.02712608  0.22790371  0.25520539  0.26671337  0.29105225  0.26161951
  0.28468075  0.26071488  0.27794551  0.29174905  0.26726898  0.28312362
  0.27094326  0.2082082   0.25459638  0.2834199   0.26995972  0.24313251
  0.07029453  0.28404042  0.22767966  0.10387403  0.27088747  0.28205749
  0.21657764  0.26775535  0.28957931  0.28127903  0.20324686 -0.01019032
  0.21616488  0.20440113  0.2115379   0.28796184  0.25000729  0.2732134
  0.2618875   0.17617432]

따라서, 아래와 같이 Outlier의 실제 Anomaly Score는 $0.51019$로, $0.5$보다 크기 때문에 Outlier로 판정한 것을 볼 수 있습니다.

print(0.5-IsF.decision_function(X)[27600 : 27650])
--------------------------------------------------------------------------------------------------------------------------------
[0.20498682 0.24553298 0.23157304 0.21871498 0.24151007 0.3229185
 0.24161616 0.35998103 0.28487541 0.2958676  0.21059554 0.21663613
 0.47287392 0.27209629 0.24479461 0.23328663 0.20894775 0.23838049
 0.21531925 0.23928512 0.22205449 0.20825095 0.23273102 0.21687638
 0.22905674 0.2917918  0.24540362 0.2165801  0.23004028 0.25686749
 0.42970547 0.21595958 0.27232034 0.39612597 0.22911253 0.21794251
 0.28342236 0.23224465 0.21042069 0.21872097 0.29675314 0.51019032
 0.28383512 0.29559887 0.2884621  0.21203816 0.24999271 0.2267866
 0.2381125  0.32382568]

얼마나 예측이 맞았는지 확인해보도록 하겠습니다. 우선 시각화를 해보았을 때, 위쪽 Raw Data 시각화와 비교해보면 잘 맞게 예측한 부분도 있고, 아닌 부분도 있는 것 같습니다!

fig = go.Figure()
fig.add_trace(go.Scatter(x = data['V3'], y = data['V4'], mode = "markers", marker_color = y_pred2['y_pred'], marker_colorscale = "Bluered_r"))
my_font = 'Times New Roman'
fig.update_layout(legend = dict(y = 0.5, font_size = 20, font_family = my_font), title = 'Credit Card Fraud Detection (Prediction)', title_font_family = my_font, font_size = 20, title_x = 0.5)
fig.update_layout(margin = dict(l = 0, r = 0, t = 60, b = 0), width = 800, height = 600)
fig.update_xaxes(title_text = 'V3', title_font_family = my_font)
fig.update_yaxes(title_text = 'V4', title_font_family = my_font)

fig.show()

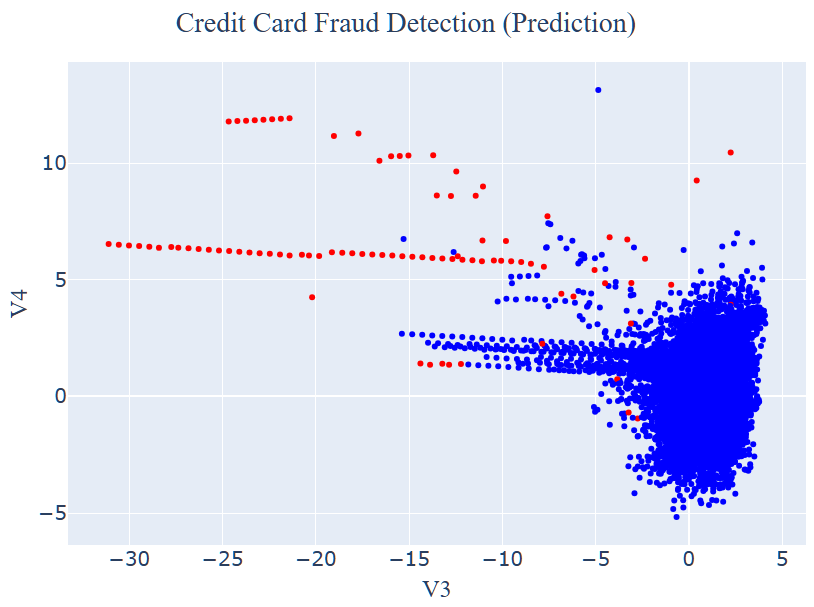
image-20241117214738357

그래서 classification_report로 확인해 보았을 때, F1-score가 0.48로 다소 아쉬운 성능을 보여주는 것을 확인했습니다. 그렇지만 실제 금융 데이터이고, 아무런 전처리를 하지 않은 상태라는 것을 감안했을 때, 이 정도 성능은 나쁘지 않은 것이라고 판단했습니다.

from sklearn.metrics import classification_report

y_pred2.loc[y_pred2['y_pred'] == 1, :] = 0 
y_pred2.loc[y_pred2['y_pred'] == -1, :] = 1
print(classification_report(y['Class'], y_pred2['y_pred']))
--------------------------------------------------------------------------------------------------------------------------------
              precision    recall  f1-score   support

           0       1.00      1.00      1.00     29786
           1       0.48      0.48      0.48        94

    accuracy                           1.00     29880
   macro avg       0.74      0.74      0.74     29880
weighted avg       1.00      1.00      1.00     29880

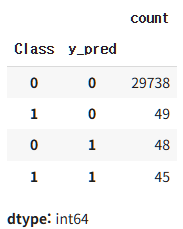
94개 중 45개의 Fraud를 맞힌 것을 확인할 수 있습니다.

y_data = pd.concat([y, y_pred2], axis = 1)
y_data.value_counts()

image-20241117215649919


Reference

  1. 김성범[교수/산업경영공학부]
  2. 김성범[교수/산업경영공학부]
  3. Fast Campus : 30개 사례로 배우는 Anomaly Detection 알고리즘 구현과 실전 프로젝트 Online
  4. vvakki_.log
  5. 파이썬을 이용한 통계적 머신러닝    [박유성 지음]


DATA_100%_LOGO_LIGHT



댓글남기기

참고

[연속형 분포] 코시 분포

안녕하세요! 최근 AI 기법들에 대해 설명 드렸었는데 잠시 쉬어가는 의미로 오랜만에 수리통계학 분포 시리즈로 돌아왔습니다. 올해 마지막 포스팅으로 코시 분포에 대해 설명드리도록 하겠습니다.

[Anomaly Detection] LOF

이번 시간부터는 드디어 Anomaly Detection으로 넘어가보도록 하겠습니다. 평소에 이상탐지에 관심이 많았는데 재밌고 새로운 사실도 알게되서 너무 좋네요! 😄 Anomaly Detection 파트의 첫 번째 시간이기 때문에 간단히 이상탐지에 대해 알아보고, 밀도 기반 이...

[Sampling] Mixed sampling

이번 시간에는 Sampling의 마지막 포스트인 Mixed Sampling에 대해 알아보겠습니다. 즉, 앞서 설명드린 UnderSampling과 OverSampling을 모두 이용하는 Sampling 기법입니다. 간단히 2가지 정도를 소개하고 Sampling Chapter를 마...

[Sampling] Oversampling

안녕하세요. 지난 포스트인 UnderSampling에 이어서 Sampling 기법 중 하나인 OverSampling에 대해 알아보겠습니다. 일반적으로 머신러닝에서 UnderSampling보다 많이 사용되며, 4가지 정도 소개하도록 하겠습니다.