[연속형 분포] 정규 분포

이번 시간에는 통계학을 다루는데 있어서 정말 정말 정말 중요한 정규 분포에 대해 알아보겠습니다. 앞으로의 계획을 말씀드리자면, 원래는 이번 포스트를 끝으로 연속형 분포 포스팅을 끝내려고 했으나, 중심극한정리를 따로 포스팅하고, 와이블 분포까지 다루려고 합니다. 이후로는 통계 분포 포스팅을 잠시 멈추고, 공부하고 있는 Pytorch에 대해 정리하여 올리겠습니다! 지난 주는 일본으로 가족 여행이 있어서 포스팅을 못했었네요. 😁

정의

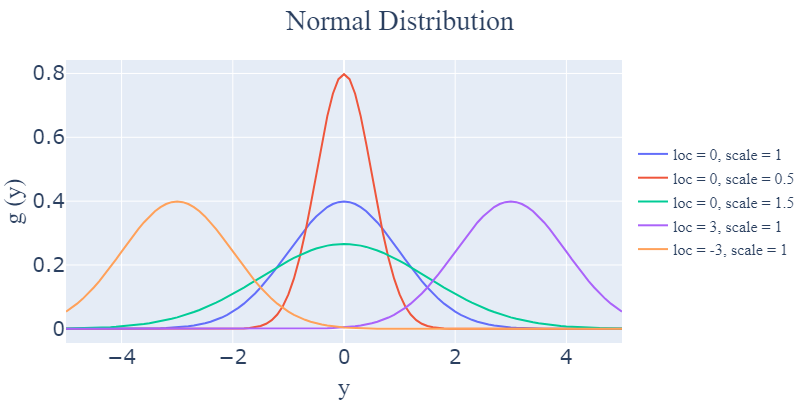
고등수학 확률과 통계 파트에서부터 공부했던 정규분포(Normal Distribution)에 대해 알아보도록 하겠습니다. 정규분포는 통계학에서 가장 많이 활용되는 확률분포입니다. 범위는 $(-\infty, \infty)$이며, 평균을 중심으로 대칭인 종 모양으로 그려집니다. 분산이 커질수록 봉우리가 낮아지고, 꼬리 부분이 두꺼워집니다.

$X~{\sim}~N(\mu, \sigma^{2})$인 정규분포의 pdf는 아래와 같습니다. 수식이 다소 복잡합니다.

$ \begin{align*} f(x) &= \frac {1}{\sqrt{2\pi} \sigma}e^{-\frac {(x-\mu)^2}{2 \sigma^{2}}}, ~~~-\infty < x < \infty \\ \end{align*} $

평균이 $0$, 분산이 $1$인 정규분포를 표준정규분포(Standard Normal Distribution)라고 합니다. $Z~{\sim}~N(0, 1)$인 표준정규분포의 pdf는 아래와 같습니다.

$ \begin{align*} f(z) &= \frac {1}{\sqrt{2\pi}}e^{-\frac {z^2}{2}}, ~~~-\infty < z < \infty \\ \end{align*} $

정규분포의 대의적 정의는 아래와 같습니다. 이에 대한 자세한 증명은 아래의 MGF를 이용하여 증명할 수 있습니다.

$X~{\sim}~N(\mu, \sigma)~~\Leftrightarrow~~\frac{X - \mu}{\sigma}~{\sim}~N(0, 1)~~\Leftrightarrow~~ X\overset{\mathrm{d}}{\equiv}\sigma Z + \mu,~~Z~{\sim}~N(0, 1) $

위와 같이 복잡한 pdf에서 과연 $-\infty < z < \infty$ 구간에서 적분했을 때, $1$을 만족하는지 알아보겠습니다. 극좌표 변환을 활용하면 쉽게 증명할 수 있습니다. ($Z~{\sim}~N(0, 1)$인 표준정규분포에 한해서 증명해 보았습니다.)

$ \begin{align*} (Let. ~~~~I &= \int_{-\infty}^{\infty} \frac {1}{\sqrt{2\pi}}e^{-\frac {z^2}{2}} ~dz) \\ I^{2} &= \frac {1}{2\pi} [\int_{-\infty}^{\infty}e^{-\frac {x^2}{2}} ~dx][\int_{-\infty}^{\infty}e^{-\frac {y^2}{2}} ~dy] \\ &= \frac {1}{2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-\frac {x^{2} + y^{2}}{2}} ~dxdy \\ \\ \\ (Let. ~~~~x &= r~cos\theta,~~~y = r~sin\theta) \\ \therefore |J| &= r(sin^{2}\theta + cos^{2}\theta) = r \\ \\ \\ I^{2} &= \frac {1}{2\pi} \int_{0}^{2\pi} \int_{0}^{\infty} r e^{-\frac {r^{2}}{2}} ~drd\theta \\ &= \frac {1}{2\pi} \int_{0}^{2\pi} \int_{0}^{\infty} e^{-t} ~dtd\theta ~~~~(Let.~~~~t= \frac{r^2}{2}) \\ &= \frac {1}{2\pi} \int_{0}^{2\pi} d\theta \\ &= 1 \\ \\ \therefore I &= 1 ~~~~(\because I > 0) \\ \end{align*} $

특징

평균과 분산을 구해보도록 하겠습니다. $X~{\sim}~N(\mu, \sigma^{2})$에서 과연 $X$의 기댓값이 실제로 $\mu$인지, 그리고 분산이 $\sigma^{2}$가 맞는지 아래와 같이 증명했습니다.

$ \begin{align*} E(X) &= \int_{-\infty}^{\infty} \frac {x}{\sqrt{2\pi} \sigma}e^{-\frac {(x-\mu)^2}{2 \sigma^{2}}} ~dx \\ \\ (Let. ~~~~y &= \frac {x - \mu}{\sigma},~~~dy=\frac{1}{\sigma}dx) \\ \\ &= \int_{-\infty}^{\infty} (\sigma y + \mu) \frac {1}{\sqrt{2\pi}}e^{-\frac {y^2}{2}} ~dy \\ &= \frac {1}{\sqrt{2\pi}} [[-\sigma e^{-\frac {y^2}{2}}]^{\infty}_{-\infty} + \int_{-\infty}^{\infty} \mu e^{-\frac {y^2}{2}} ~dy] \\ &= \frac {\mu}{\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-\frac {y^2}{2}} ~dy \\ &= \frac {\sqrt{2}\mu}{\sqrt{\pi}} \int_{0}^{\infty} e^{-\frac {y^2}{2}} ~dy \\ \\ (Let. ~~~~z &= \frac {y^2}{2},~~~y~dy=dz) \\ \\ &= \frac {\sqrt{2}\mu}{\sqrt{\pi}} \int_{0}^{\infty} \frac {e^{-z}}{\sqrt{2 z}} ~dz \\ &= \frac {\sqrt{2}\mu}{\sqrt{\pi}} \times \frac{1}{\sqrt{2}} \int_{0}^{\infty} z^{\frac {1}{2} - 1} e^{-z} ~dz \\ &= \frac {\mu}{\sqrt{\pi}} \times \Gamma(\frac {1}{2}) \\ &= \frac {\mu}{\sqrt{\pi}} \times \sqrt{\pi} \\ &= \mu \\ \\ \\ Var(X) &= E(X^2) - [E(X)]^2 \\ (Let. ~~~~Z &= \frac {x - \mu}{\sigma}~{\sim}~N(0, 1),~~~~E(Z) = 0) \\ E(Z^2) &= \int_{-\infty}^{\infty} \frac {z^2}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}} ~dz \\ (Let. ~~~~W &= \frac {z^2}{2},~~~z~dz=dw \\ &= 2 \int_{0}^{\infty} \frac {z^2}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}} ~dz \\ &= 2 \int_{0}^{\infty} \frac {2w}{\sqrt{2 \pi}} \frac {e^{-w}}{\sqrt{2w}} ~dw \\ &= \frac {2}{\sqrt{\pi}} \int_{0}^{\infty} w^{\frac{3}{2} - 1}e^{-w} ~dw \\ &= \frac {2}{\sqrt{\pi}} \times \Gamma(\frac {3}{2}) \\ &= \frac {2}{\sqrt{\pi}} \times \frac {\sqrt{\pi}}{2} \\ &= 1 \\ \\ Var(Z) &= 1 - 0^2 = 1 \\ \therefore Var(X) &= Var(\sigma Z) = \sigma^{2} \\ \end{align*} $

또한, MGF 증명을 아래와 같이 정리했습니다. $(X~{\sim}~N(\mu, \sigma^{2}), Z~{\sim}~N(0, 1))$

$ \begin{align*} M_{Z}(t) &= E(e^{tz}) \\ &= \int_{-\infty}^{\infty} \frac {1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}} e^{tz} ~dz \\ &= \int_{-\infty}^{\infty} \frac {1}{\sqrt{2 \pi}} e^{-\frac{(z-t)^2}{2}} ~dz \times e^{\frac {t^2}{2}} \\ &= e^{\frac {t^2}{2}},~~~~-\infty < t < \infty \\ M_{X}(t) &= E(e^{tx}) \\ &= E(e^{t(\sigma z + \mu)}) \\ &= e^{t \mu} \times e^{\frac {(t \sigma)^2}{2}} \\ &= e^{t \mu + \frac {\sigma^2 t^2}{2}},~~~~-\infty < t < \infty \\ \end{align*} $

위의 증명으로 알 수 있는 사실은 정규확률변수는 선형변환을 해도 역시 정규분포를 따른다는 점입니다. 예를 들어 $X~{\sim}~N(\mu, \sigma^{2})$일 때, $Y = aX + b$라면 MGF의 분포결정성으로부터 $Y~{\sim}~N(a \mu + b, a^2 \sigma^{2})$를 따른다는 것을 아래와 같이 증명할 수 있습니다.

$ \begin{align*} M_{Y}(t) &= M_{aX + b}(t) \\ &= \int_{-\infty}^{\infty} \frac {1}{\sqrt{2 \pi}} e^{-\frac{z^2}{2}} e^{tz} ~dz \\ &= e^{bt + \mu(at) + \frac {1}{2} \sigma^{2} (at)^2} \\ &= e^{(a \mu + b)t + \frac {1}{2}(a^2 \sigma^{2}) t^2},~~~~-\infty < t < \infty \\ \end{align*} $

다음 포스트는 이렇듯 복잡한 정규분포가 통계학에서 왜 중요한 위치해 있는지, 중심극한정리란 무엇인지 설명드리겠습니다!

Reference

1. 수리통계학    [송성주, 전명식 지음]
2. 수리통계학    [김우철 지음]
3. 서울시립대학교 수리통계학 I 수업    [정병철 교수님]
4. 고려대학교 추론통계학 I 수업    [송성주 교수님]