[연속형 분포] 와이블 분포
안녕하세요! 수리통계학 분포 시리즈의 마지막 포스트로 와이블 분포에 대해 설명드리겠습니다. 이 외에도 수많은 분포들이 많지만 우선은 여기까지 다루고 나중에 추가로 다루도록 하겠습니다.
정의
사실 와이블 분포(Weibull Distribution)는 대학교의 수리통계학에서 많이 다뤄지는 분포는 아닙니다. 그럼에도 불구하고 설명드리는 이유는 제가 재직하고 있는 제조업계에서 아직까지 많이 사용하고 있는 분포이기 때문입니다. $X~{\sim}~Weibull(k, \lambda)$에서의 pdf는 아래와 같습니다.
$ \displaystyle{ f(x ; k, \lambda) = \frac {k} {\lambda} (\frac {x} {\lambda})^{k - 1} e^{-(\frac {x} {\lambda})^{k}} }$
pdf는 형상모수 $k$와 척도모수 $\lambda$로 이루어져 있습니다. 이 중 와이블 분포의 형태에 더 큰 역할을 하는 모수는 형상모수 $k$입니다. 와이블 분포는 다른 분포와 비교했을 때, 형상모수의 값에 따라서 그래프의 형태가 상당히 달라집니다. 이러한 유연한 형태의 특징으로 제조업계에서는 수명 데이터 분석, 고장 예측 등에서 많이 사용하고 있습니다. 물론 최근에는 데이터 수가 방대해지면서 머신러닝, 딥러닝 기법을 사용할 수도 있지만, 적은 데이터를 가지고 있을 때는 통계 분석인 와이블 분포 생존 분석이 훨씬 좋은 인사이트를 제공하기도 합니다. 생존분석에 대한 자세한 내용은 나중에 정리해서 포스팅하겠습니다.
특징
와이블 분포의 평균과 분산을 구해보도록 하겠습니다.
$ \begin{align*} E(X) &= \int_{0}^{\infty} x \cdot \frac {k}{\lambda}(\frac {x}{\lambda})^{k-1}e^{-(\frac {x}{\lambda})^{k}} ~dx \\ &= \int_{0}^{\infty} \lambda \cdot u^{\frac{1}{k}} \cdot e^{-u} ~du ~~~({\rm Let.}~~u=(\frac{x}{\lambda})^{k},~~du=\frac{k}{\lambda}(\frac{x}{\lambda})^{k-1}dx)\\ &= \lambda \cdot \Gamma(\frac{1}{k}+1) \\ \\ E(X^2) &= \int_{0}^{\infty} x^{2} \cdot \frac {k}{\lambda}(\frac {x}{\lambda})^{k-1}e^{-(\frac {x}{\lambda})^{k}} ~dx \\ &= \int_{0}^{\infty} (\lambda \cdot u^{\frac{1}{k}})^{2} \cdot e^{-u} ~du ~~~({\rm Let.}~~u=(\frac{x}{\lambda})^{k},~~du=\frac{k}{\lambda}(\frac{x}{\lambda})^{k-1}dx) \\ &= \lambda^{2} \int_{0}^{\infty} u^{\frac{2}{k}} e^{-u} ~du \\ &= \lambda^{2} \cdot \Gamma(\frac{2}{k}+1) \\ \\ \therefore Var(X) &= E(X^2) - [E(X)]^2 \\ &= \lambda^{2} \Gamma(\frac{2}{k}+1) - \lambda^{2} [\Gamma(\frac{1}{k}+1)]^{2} \\ &= \lambda^{2} [\Gamma(\frac{2}{k}+1) - [\Gamma(\frac{1}{k}+1)]^{2}] \\ \end{align*} $
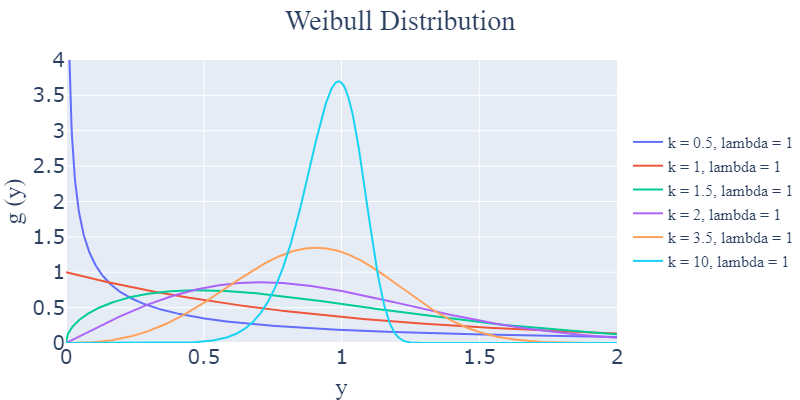
또한, 형상모수에 따라 그래프가 어떻게 달라지는 지 설명드리겠습니다. $k$는 형상모수를 의미합니다! 또한, 어느 제조업계의 특정 기계 부품의 가동시간이 와이블 분포를 따른다고 가정하여 해석하겠습니다.
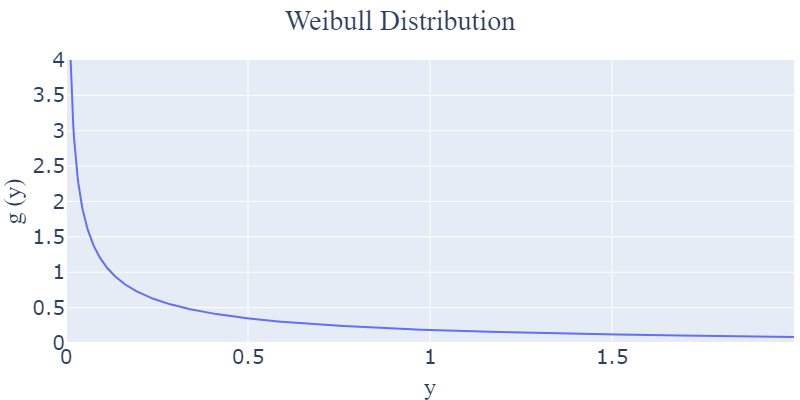
- $0 < k < 1$ : 초기 고장 횟수가 매우 높음
-> 우측의 그래프는 초기 생산된 기계 부품의 가동 시간에서 많이 나타납니다. 만약 어느 정도 생산이 된 부품임에도 와이블 분포가 오른쪽과 같이 그려진다면, 커다란 품질 문제가 발생했다는 것을 의미하겠죠? 이렇게 제조업계에서는 도출되는 형상 모수를 해석하면서 후속 의사 결정을 진행합니다!
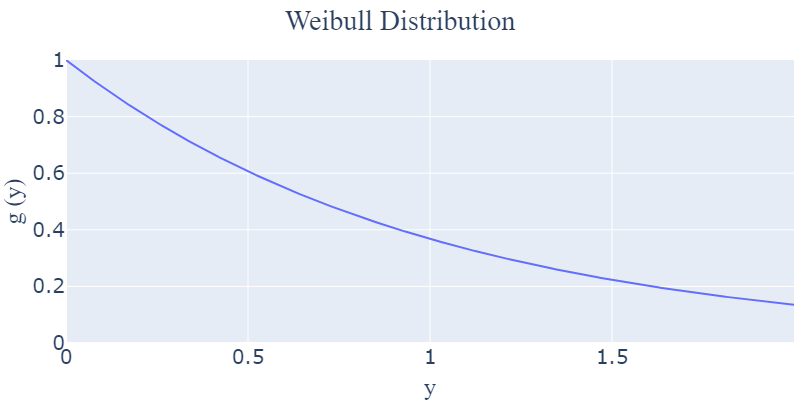
- $k = 1$ : 지수 분포
-> $k = 1$이 되면 지수 분포가 됩니다. 이는 시간이 지나면서 고장률이 일정하게 유지됨을 의미하며, 무작위 및 복합적인 원인에 의한 고장이 발생했다는 것으로 해석합니다.
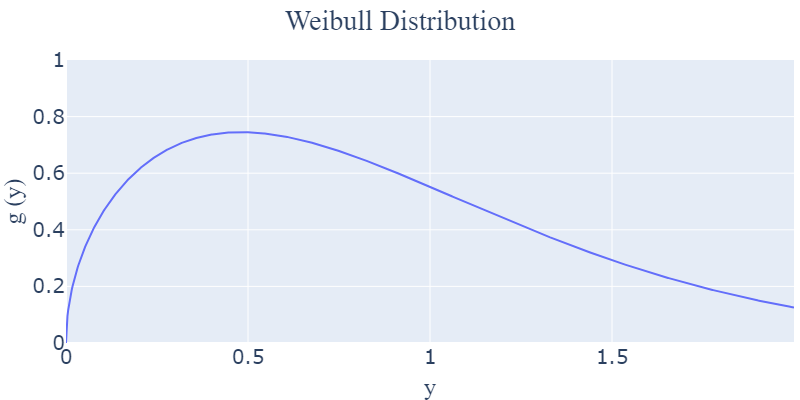
- $1 < k < 2$
-> 고장률이 전반적으로 증가하며, 가동 시간 초기에 가장 급격하게 증가합니다. 일반적으로 초기 마모 고장 부품의 가동시간이 이러한 그래프를 그립니다.
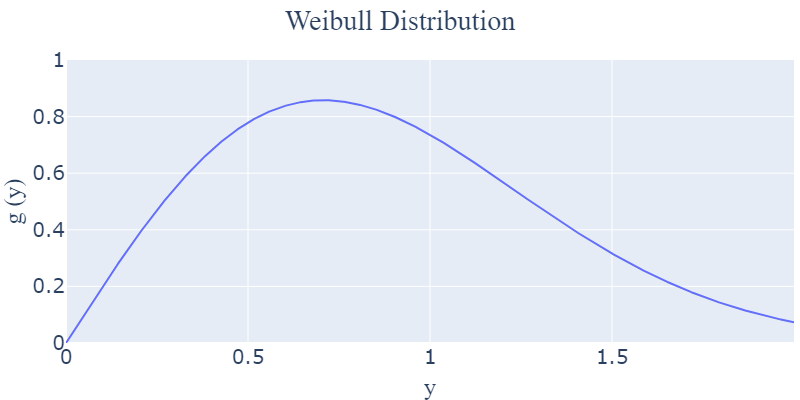
- $k = 2$
-> 선형적으로 고장률이 증가하는 것을 의미합니다. 부품 수명이 증가할수록 고장의 위험도 꾸준히 증가합니다. 추가적으로 와이블 분포에서 $k = 2$인 분포를 레일리(Rayleigh) 분포라고도 부릅니다.
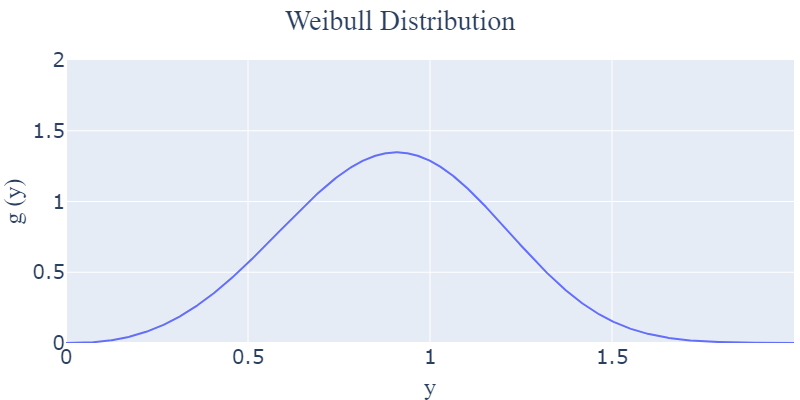
- $3 < k < 4$
-> 점점 종 모양의 대칭형인 정규 분포와 가까워지는 것을 볼 수 있습니다. 대부분의 기계 부품들의 마지막 수명 기간 동안 발생하는 급격한 마모 고장을 모델링합니다.
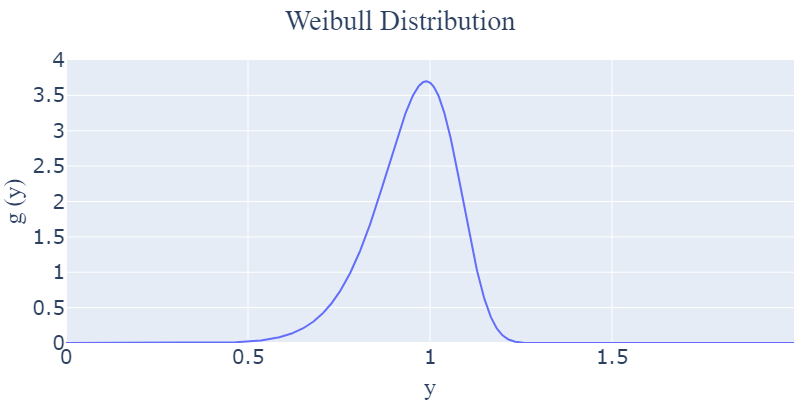
- $k > 10$
-> 일반적인 기계부품보다는 매우 빠른 마모 고장 기간으로 들어선 기계부품의 최종 기간을 모델링합니다.
이렇게 통계 분포에 대한 포스팅을 마치도록 하겠습니다. 다음 시간부터는 공부하고 있는 Pytorch에 대해 포스팅을 하도록 하겠습니다!
Reference

댓글남기기