[연속형 분포] 코시 분포

안녕하세요! 최근 AI 기법들에 대해 설명 드렸었는데 잠시 쉬어가는 의미로 오랜만에 수리통계학 분포 시리즈로 돌아왔습니다. 올해 마지막 포스팅으로 코시 분포에 대해 설명드리도록 하겠습니다.

정의

코시분포(Cauchy Distribution)는 일반적으로 학부 통계학에서 많이 다뤄지는 분포는 아닙니다. 저도 코시 분포에 대해 본격적으로 알게 된 것은 통계대학원에 진학했을 때였습니다.

이전에 정규분포에 대해 포스팅했던 적이 있습니다. 정규분포의 특징 중 하나는 서로 다른 두 정규분포가 독립관계에 있을 때, 두 정규분포의 합도 역시 정규분포를 따른다는 것입니다. 그렇다면 $iid$ 관계에 있는 두 정규분포를 서로 나눠버리면 어떤 분포가 될까요? 바로 코시분포를 따르게 됩니다. (증명은 생략하도록 하겠습니다.) 편의를 위해 뒷 내용부터는 표준코시분포에 대해서 설명드리도록 하겠습니다. $X~{\sim}~Cauchy(0, 1)$에서의 pdf는 아래와 같습니다.

$ \displaystyle{ f(x) = \frac {1} {\pi} \frac {1} {x^{2}+1} },~~~-\infty<x<\infty$

이어서 위의 pdf가 $-\infty < z < \infty$ 구간에서 적분했을 때, $1$을 만족하는지 알아보겠습니다.

$ \begin{align*} \int_{-\infty}^{\infty} \frac {1} {\pi} \frac {1} {x^{2}+1} ~dx &= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac {1} {\pi} \frac {1} {\rm {tan^{2}\theta}+1} \rm {sec^{2}\theta}~d\theta ~~~({\mathrm Let.}~~x={\mathrm tan\theta},~~dx={\rm sec^{2}\theta}d\theta) \\ &= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac {1} {\pi} ~d\theta ~~~(\because {\rm {tan^{2}\theta}+1} = {\rm sec^{2}\theta}) \\ &= \frac {1}{\pi} \cdot {\pi} \\ &= 1 \\ \end{align*} $

특징

코시 분포의 가장 큰 특징은 평균과 분산이 존재하지 않는다는 점입니다. 조금 더 확장되서 말씀드리자면 적률 자체가 존재하지 않죠. 제일 아래 이미지를 보면, 분명 $0$을 기준으로 정규분포와 비슷한 대칭형의 종 모양의 그래프가 그려집니다. 하지만 그럼에도 불구하고 평균은 $0$이 아닙니다. 아예 구할 수가 없죠. 한번 직접 평균을 구해보도록 하겠습니다.

$ \begin{align*} E(X) &= \int_{-\infty}^{\infty} \frac {1} {\pi} \frac {x} {x^{2}+1} ~dx \\ &= \int_{-\infty}^{0} \frac {1} {\pi} \frac {x} {x^{2}+1} ~dx + \int_{0}^{\infty} \frac {1} {\pi} \frac {x} {x^{2}+1} ~dx\\ &= \int_{1}^{\infty} \frac {1} {\pi} \frac {1} {2t} ~dt + \int_{\infty}^{1} \frac {1} {\pi} \frac {1} {2t} ~dt ~~~({\rm Let.}~~t=x^{2}+1,~~dt=2xdx)\\ &= \frac {1} {\pi} [\frac {1}{2} {\rm log}t]^{\infty}_{1} + \frac {1} {\pi} [\frac {1}{2} {\rm log}t]^{1}_{\infty}\\ \\ &= \infty - \infty \\ \end{align*} $

즉 $\infty - \infty$ 형태의 식이 만들어지므로, 평균은 존재하지 않는다는 결론이 나옵니다. 추가적으로 평균이 없기 때문에 분산도 구할 수가 없죠.

조금 더 일반화된 증명을 위해, 이번에는 mgf를 구해보도록 하겠습니다.

$ \begin{align*} E(e^{tX}) &= \int_{-\infty}^{\infty} e^{tx} \frac {1} {\pi} \frac {1} {x^{2}+1} ~dx \\ &\ge \int_{-\infty}^{\infty} tx \frac {1} {\pi} \frac {1} {x^{2}+1} ~dx ~~~(\because \rm {Mean~Value~Theorem},~~\frac{e^{tx}-e^{0}}{tx-0}>1 ~ \Leftrightarrow ~ e^{tx} > tx)\\ &= t E(X) \\ &= \infty - \infty \\ \end{align*} $

따라서, mgf도 구할 수 없으며 적률도 없다는 것이 증명됩니다.

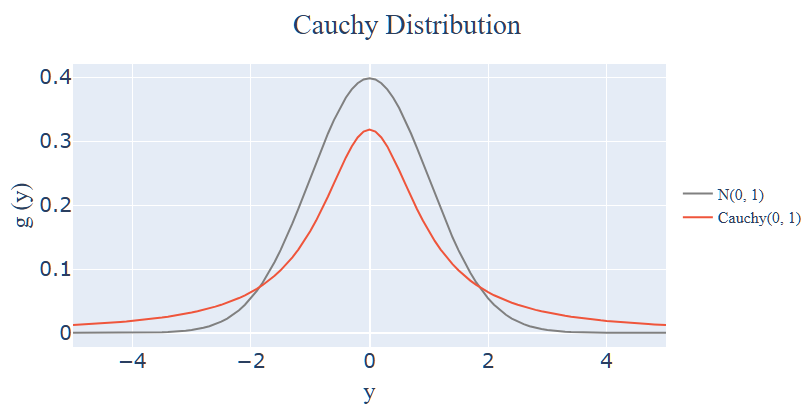
아래는 코시 분포에 대한 그래프입니다. 정규분포와 비교했을 때, 꼬리가 더 두꺼우며 종의 높이가 더 낮은 것을 알 수 있습니다.

Reference

1. 수리통계학    [김우철 지음]
2. 고려대학교 추론통계학 I 수업    [송성주 교수님]
3. Steven's AI Studylog