[이산형 분포] 포아송 분포

---

안녕하세요! 이번 시간에는 이산형 분포의 마지막 파트로 포아송 분포를 소개해드리려고 합니다. 포아송 분포를 가장 마지막에 설명드리는 이유는 일부 연속형 분포을 설명함에 있어서 포아송 분포 내용이 필요하기에 이산형과 연속형의 중간 다리 역할로서 마지막으로 설명드리게 되었습니다!

그리고 이번부터 1주일에 한 번씩 포스팅을 하려고 합니다… 최소한 2~3일에 한 번은 올리려고 했는데 현생을 살 수가 없더라구요. 솔직히 빠듯한 일정이어서 힘들었습니다😅 그래서 한 달에 4~5개 포스트를 목표로 블로그를 운영해보도록 하겠습니다.

정의

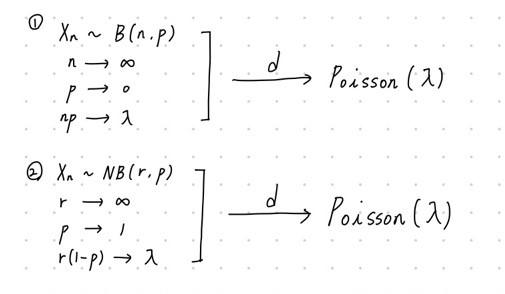
이전에 설명드렸던 이항분포로 돌아가보겠습니다. $X~{\sim}~B(n, p)$일 때, 만약 $n$이 무한대에 가깝게 커지게 된다면 어떤 분포로 근사하게 될까요? $n$이 커짐에 따라 $p$도 $0$으로 수렴하게 되어, $np=\lambda$를 만족한다면 어떻게 될지 증명해보았습니다!

$ \begin{align*} \lim_{n \rightarrow \infty} \begin{pmatrix} n\\ x \end{pmatrix} p^x (1-p)^{n-x} &= \lim_{n \rightarrow \infty} \begin{pmatrix} n\\ x \end{pmatrix} (\frac {\lambda} {n})^x (1 - \frac {\lambda} {n})^{n-x}~~~~(\because np=\lambda) \\ &= \lim_{n \rightarrow \infty} \frac {n!} {x!(n-x)!} \lambda^x (\frac {1} {n})^x (1 - \frac {\lambda} {n})^{-x} (1 - \frac {\lambda} {n})^{n} \\ &= \frac {\lambda^x} {x!} \lim_{n \rightarrow \infty} \frac {n!} {(n-x)!(n-\lambda)^{x}}(1 - \frac {\lambda} {n})^{n} \\ &= \frac {\lambda^x} {x!} \lim_{n \rightarrow \infty} (1 - \frac {\lambda} {n})^{n} \frac {n(n-1) \cdots (n-x+1)} {n^x(1 - \frac{\lambda} {n})^{x}} \\ &= \frac {\lambda^x} {x!} \lim_{n \rightarrow \infty} (1 - \frac {\lambda} {n})^{n} 1 \times (1 - \frac{1}{n}) \times (1 - \frac{2}{n}) \cdots \times (1 - \frac{x - 1}{n}) \times (1 - \frac{\lambda}{n})^{-x} \\ &= \frac {\lambda^x} {x!} \times 1 \times e^{-x}~~~~(\because (1 - \frac{\lambda}{n})^{n} \rightarrow e^{-\lambda}) \\ &= \frac {\lambda^x e^{-\lambda}} {x!} \\ \end{align*} $

위와 같은 근사를 이항확률의 포아송 근사라고 부릅니다. 그리고 아래의 수식은 포아송 분포의 pdf가 됩니다. 포아송 분포(Poisson Distribution)는 단위 시간 동안 발생하는 어떤 특정 사건의 발생횟수에 대한 확률분포를 말합니다. 예를 들어 어느 고속도로 구간에서의 교통사고 횟수, 공장 제품 중 불량 개수 등이 포아송 분포를 따를 수 있습니다.

$ f(x) = \frac {\lambda^x e^{-\lambda}} {x!},~~~~x=0,~1,~2,~\cdots $

추가적으로 $X$가 모수가 $\lambda$인 포아송분포를 따를 때, 편의상 $X~{\sim}~Poi(\lambda)$로 표기합니다.

특징

모수가 $\lambda$인 포아송 분포의 기댓값과 분산은 모두 $\lambda$입니다. 기댓값은 아래와 같이 증명할 수 있습니다.

$ \begin{align*} E(X) &= \sum_{x=0}^{\infty} x \frac {\lambda^x e^{-\lambda}} {x!} \\ &= \lambda e^{-\lambda} \sum_{x=1}^{\infty} \frac {\lambda^{x-1}} {(x-1)!} \\ &= \lambda e^{-\lambda} e^{\lambda} \\ &= \lambda \\ \end{align*} $

분산은 $Var(X)=E(X(X-1))+E(X)-(E(X)) ^{2}$식을 이용하여 구할 수 있습니다.

$ \begin{align*} E(X(X-1)) &= \sum_{x=0}^{\infty} x(x-1) \frac {\lambda^x e^{-\lambda}} {x!} \\ &= \lambda^{2} e^{-\lambda} \sum_{x=2}^{\infty} \frac {\lambda^{x-2}} {(x-2)!} \\ &= \lambda^{2} e^{-\lambda} e^{\lambda} \\ &= \lambda^{2} \\ \therefore Var(X) &= \lambda^{2} + \lambda - \lambda^{2} \\ &= \lambda \end{align*} $

적률생성함수도 기댓값과 분산을 구하는 과정과 비슷합니다!

$ \begin{align*} M_{X}(t) &= E(e^{tX}) \\ &= \sum_{x=0}^{\infty} e^{tx} \frac {\lambda^x e^{-\lambda}} {x!} \\ &= e^{-\lambda} \sum_{x=0}^{\infty} \frac {(\lambda e^{t})^x} {(x)!} \\ &= e^{-\lambda} e^{\lambda e^{t}}\\ &= e^{\lambda(e^{t} - 1)},~~~~-\infty < t < \infty \\ \end{align*} $

또한, 따로 증명 내용을 담지 않겠지만 포아송 근사에 대한 내용을 아래와 같이 정리했습니다.

Reference

1. 수리통계학    [송성주, 전명식 지음]
2. 수리통계학    [김우철 지음]
3. 서울시립대학교 수리통계학 I 수업    [정병철 교수님]
4. 고려대학교 추론통계학 I 수업    [송성주 교수님]