[연속형 분포] 균일 분포

---

안녕하세요! 지난 주는 친구들과 여행으로 포스팅을 못했습니다. 속초가서 힐링 잔뜩하고 왔어용 😁 그리고 다음 주와 다다음 주에는 회사 미국 출장으로 포스팅을 못할 가능성이 높습니다. 결국 5월에는 글을 1개밖에 못 올리겠네요… 😥 이번 시간에는 균일 분포를 소개드립니다. 어찌보면 연속형 분포 중 가장 간단한 pdf를 가지고 있는 분포입니다. 추가적으로 균일 분포와 관련된 분포 몇 개를 정리했습니다.

정의

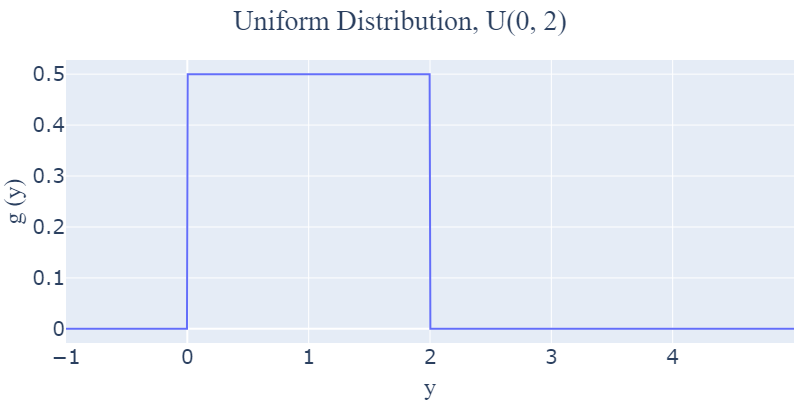
확률변수 $X$가 특정 실구간 상에 균일하게 분포되어 있을 때 $X$는 균일 분포(Uniform Distribution)를 따릅니다. 즉, 특정 실구간 내에서 $X$의 값이 무엇이 되더라도 pdf 값이 일정합니다. pdf는 아래와 같이 도출되고, $X~{\sim}~U(a, b)$로 표기합니다.

$ \begin{align*} f(x) &= \frac {1}{b - a}, ~~~a < x < b \\ \end{align*} $

만약, $X~{\sim}~U(a, b) , Z~{\sim}~U(0, 1)$라고 한다면 아래와 같은 정의로 표현할 수 있습니다.

$X\overset{\mathrm{d}}{\equiv}(b - a)Z + a $

특징

이번엔 $X~{\sim}~U(a, b)$인 $X$의 기댓값과 분산을 직접 구하지 않고, $Z~{\sim}~U(0, 1)$를 이용하여 기댓값과 분산을 구해보겠습니다. $Z$의 평균과 분산은 아래와 같습니다.

$ \begin{align*} E(Z) &= \int_{0}^{1} z ~dz \\ &= \frac {1}{2} \\ E(Z^2) &= \int_{0}^{1} z^2 ~dz \\ &= \frac {1}{3} \\ \therefore Var(Z) &= E(Z^2) - [E(Z)]^2 \\ &= \frac {1}{3} - \frac {1}{4} \\ &= \frac {1}{12} \\ \end{align*} $

따라서, $X$의 평균과 분산은 이전에 설명했던 정의를 이용하여 쉽게 구할 수 있습니다.

$ \begin{align*} E(X) &= E((b-a)Z + a) \\ &= \frac {(b - a)}{2} + a \\ &= \frac {(a + b)}{2} \\ Var(X) &= Var((b - a)Z + a) \\ &= \frac {(b - a)^2}{12} \\ \end{align*} $

$X$의 적률생성함수도 $Z~{\sim}~U(0, 1)$를 이용하여 구해봅시다!

$ \begin{align*} M_{Z}(t) &= E(e^{tZ}) \\ &= \int_{0}^{1} e^{tz} ~dx \\ &= \frac {e^t-1}{t}, ~~~t \neq 0 \\ \therefore M_{X}(t) &= E(e^{tX}) \\ &= E(e^{t((b - a)Z + a)}) \\ &= E(e^{ta + t(b - a)Z}) \\ &= e^{ta} \times \frac {e^t(b - a)-1}{t(b - a)} \\ &= \begin{cases}\frac {e^{tb} - e^{ta}}{t(b - a)} & t \neq 0 \\ 1 & t = 0 \end{cases} \\ \end{align*} $

추가적으로 균일 분포와 연관 있는 분포 몇 개를 소개드릴까 합니다. 이산형 분포로 이산 균등 분포(Discrete Uniform)가 있습니다. 균일 분포와 같이 확률변수 값에 따라 pdf 값이 일정하나, 연속형이 아닌 이산형 분포입니다. $X~{\sim}~Discrete ~~Uniform(a, b)$에 대한 pdf는 아래와 같습니다.

$ \begin{align*} f(x) &= \frac {1}{b - a + 1}, ~~~x = a, ~a + 1, ~\dots, ~b \\ \end{align*} $

평균과 분산은 아래와 같습니다. 평균은 균일 분포와 값이 같고 쉽게 구할 수 있으나, 분산은 수식이 꽤 복잡합니다. 자세한 증명 과정은 다루지 않겠습니다.

$ \begin{align*} E(X) &= \frac {(a + b)}{2} \\ Var(X) &= \frac {(b - a + 1)^2 - 1}{12} \\ \end{align*} $

또한, 서로 독립인 확률변수 $Z_1, ~Z_2~{\sim}~U(0, 1)$에 대하여 $Y = \frac {(Z_1 + Z_2)}{2}$ 확률변수를 생각할 수 있습니다. 이 때, $Y$는 삼각 형태의 pdf를 가지는 삼각분포(Triangular Distribution)를 따르게 됩니다. ($Y~{\sim}~\triangle(0, 1)$)

텀이 좀 길지만… 6월에 베타분포로 돌아오겠습니다!

Reference

1. 수리통계학    [송성주, 전명식 지음]
2. 수리통계학    [김우철 지음]
3. 서울시립대학교 수리통계학 I 수업    [정병철 교수님]
4. 고려대학교 추론통계학 I 수업    [송성주 교수님]