안녕하세요. 오랜만에 인사드리는 것 같습니다. 그 동안 올렸었던 수리통계학 통계분포 포스팅을 마치고, Pytorch에 대해 포스팅을 하도록 하겠습니다!! 😁😁 작년 12월부터 조금씩 공부하고 있었고, 제가 잘 알지 못했던 내용들 위주로 정리하여 올리려고 합니다. 참고로 공부는 위키독스의 [Pytorch로 시작하는 딥러닝 입문]으로 했으며, 이번 시간에는 간단히 2장 내용 초반 부분에 대해 설명드리겠습니다.

2-1. 파이토치 패키지의 기본 구성

파이토치 패키지는 크게 아래와 같이 6개의 부분으로 구성되어 있습니다. 1번을 제외하고 나머지 부분의 사용은 3장부터 정리하여 제공할 예정입니다.

  1. torch
    • 메인 네임스페이스
      • (네임스페이스 : 변수 이름, 함수 이름과 같이 명칭을 사용하는 공간, 소속을 나타냅니다.)
    • 다양한 수학 함수 포함 (numpy, pandas와 비슷한 역할을 합니다.)
  2. torch.autograd
    • 자동 미분을 위한 함수 포함
      • 콘텍스트 매니저(enable_grad/no_grad) : 자동 미분의 on/off를 제어합니다.
      • Function : 자체 미분 가능 함수를 정의할 때 사용하는 기반 클래스입니다.
  3. torch.nn
    • 신경망을 구축하기 위한 다양한 데이터 구조나 레이어로 구성
      • Layor : RNN, LSTM 등
      • 활성화 함수 : ReLU
      • 손실함수 : MSELoss
  4. torch.optim
    • 파라미터 최적화 알고리즘 구현
      • 확률적 경사 하강법(Stochastic Gradient Descent, SGD)
  5. torch.utils.data
    • SGD의 반복 연산을 실행할 때 사용하는 미니 배치용 유틸리티 함수 포함
  6. torch.onnx
    • ONNX의 포맷으로 모델을 export할 때 사용
      • ONNX(Open Neural Network Exchange) : 서로 다른 딥 러닝 프레임워크 간에 모델을 공유할 때 사용하는 포맷

2-2. 텐서 조작하기 1

1차원의 데이터를 벡터(Vector), 2차원의 데이터를 행렬(Matrix)라고 부릅니다. 텐서(Tensor)는 데이터가 3차원 이상일 때를 의미합니다. 그러나 1차원, 2차원 일 때도 1D 텐서, 2D 텐서라고 부르기도 합니다.


2D 텐서

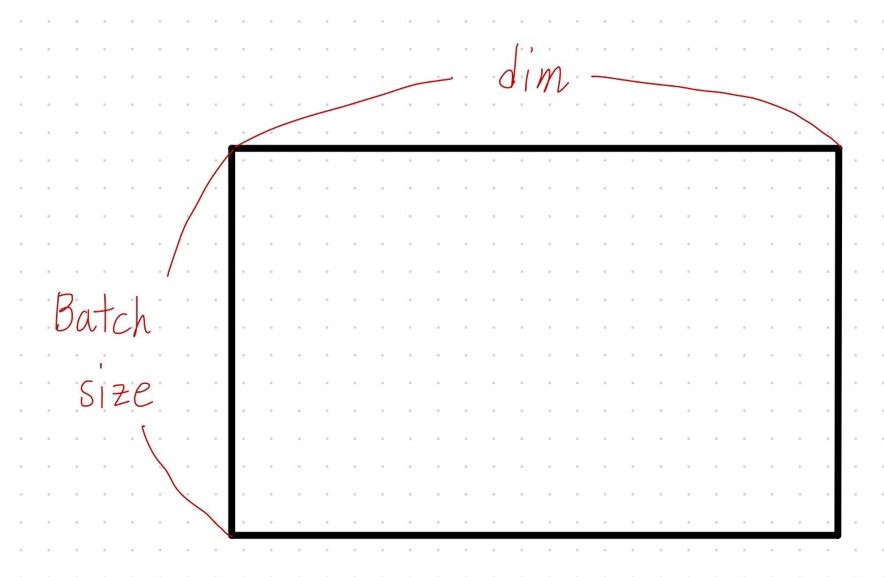
  • 2D 텐서 : (Batch size, dim)

    2차원 데이터는 위와 같이 나타낼 수 있습니다. 행의 개수를 Batch size, 열의 개수를 dim으로 표현합니다. 배치 크기를 의미하는 Batch size는 훈련 데이터의 개수가 굉장히 많을 때, 컴퓨터가 한 번에 들고 가서 처리할 양을 의미합니다. 예시를 들어보겠습니다.

    $[1, 2, 3, 4, \cdots]$와 같은 훈련 데이터 하나의 크기가 $128$이라고 가정하겠습니다. 데이터 개수가 $1000$개라고 한다면, 현재 훈련 데이터의 전체 크기는 $(1000, 128)$입니다. 여기서 컴퓨터는 데이터를 하나씩 처리하지 않고 $32, 64, 128$과 같이 $2$의 거듭제곱 개수의 묶음으로 처리합니다. 만약 $64$개씩 처리한다고 하면 Batch size는 $64$가 되고, 2D 텐서의 크기는 $(64, 128)$가 됩니다.


3D 텐서

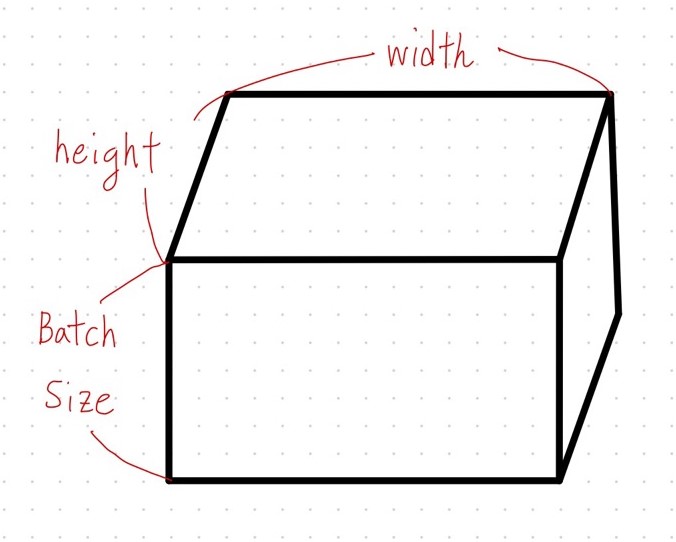
  • 3D 텐서 : (Batch size, width, height) or (Batch size, 문장 길이, 단어 벡터의 차원)

    3D 텐서는 주로 이미지, 시계열, 자연어 데이터에서 많이 사용됩니다.



이제 Torch 패키지 내 함수들에 대해 알아보겠습니다.


1. 1D with PyTorch

먼저 파이토치를 선언해줘야 합니다. 저의 경우는 컴퓨터가 GPU가 아닌 CPU이므로 Anaconda Prompt에 conda install pytorch torchvision torchaudio cpuonly -c pytorch를 입력하여 다운로드했습니다. 이후에 import를 실행합니다.

# 파이토치 선언
import torch

1차원 Tensor인 벡터를 만들어 보겠습니다. FloatTensor는 Float 형태의 Tensor를 생성합니다. 값 바로 뒤에 ‘.’이 없더라도 ‘.’이 뒤에 있는 Float 형태로 만들어집니다.

t1 = torch.FloatTensor([0., 2., 4., 6., 8.])
print('t1 :', t1)
t2 = torch.FloatTensor([0, 2, 4, 6, 8])
print('t2 :', t2)
--------------------------------------------------------------------------------------------------------------------------------
t1 : tensor([0., 2., 4., 6., 8.])
t2 : tensor([0., 2., 4., 6., 8.])

dim은 텐서의 차원, shape와 size는 텐서의 전체 크기를 알 수 있습니다.

print(t1.dim()) # 차원
print(t1.shape) # 크기
print(t1.size()) # 크기
--------------------------------------------------------------------------------------------------------------------------------
1
torch.Size([5])
torch.Size([5])

슬라이싱은 numpy와 같습니다.

print(t[0], t[1], t[-1])
print(t[2 : 5], t[3 : -1])
print(t[: 2], t[3 :]) 
--------------------------------------------------------------------------------------------------------------------------------
tensor(0.) tensor(2.) tensor(8.)
tensor([4., 6., 8.]) tensor([6.])
tensor([0., 2.]) tensor([6., 8.])


2. 2D with PyTorch

2차원 Tensor인 행렬을 만들어 보겠습니다.

t3 = torch.FloatTensor([[1., 2., 3., 4., 5.],
                       [6., 7., 8., 9., 10.],
                       [11., 12., 13., 14., 15.],
                       [16., 17., 18., 19., 20.]])
print(t3)
--------------------------------------------------------------------------------------------------------------------------------
tensor([[ 1.,  2.,  3.,  4.,  5.],
        [ 6.,  7.,  8.,  9., 10.],
        [11., 12., 13., 14., 15.],
        [16., 17., 18., 19., 20.]])

텐서의 차원과 크기를 아래와 같이 확인할 수 있습니다.

print(t3.dim())
print(t3.shape) 
print(t3.size())
--------------------------------------------------------------------------------------------------------------------------------
2
torch.Size([4, 5])
torch.Size([4, 5])


3. 브로드캐스팅 (Broadcasting)

불가피하게 크기가 다른 행렬이나 텐서에 대해 사칙 연산을 수행할 경우가 생길 수 있습니다. 이를 위해 파이토치에서는 자동으로 크기를 맞춰서 연산을 수행하게 만드는데 이를 브로드캐스팅이라고 합니다. 아래와 같이 크기가 같을 때에는 정상적인 연산이 작동합니다.

m1 = torch.FloatTensor([[1, 1]])
m2 = torch.FloatTensor([[2, 2]])
print(m1 + m2)
--------------------------------------------------------------------------------------------------------------------------------
tensor([[3., 3.]])

이번에는 크기가 다른 텐서들의 연산을 보겠습니다. 수학적으로는 연산이 안 되는게 맞지만, 파이토치에서는 브로드캐스팅을 통해 연산합니다! 즉, m1의 크기가 (1, 2), m2의 크기가 (1,)이므로, [3]이 [3, 3]으로 변환되어 연산을 진행합니다.

m1 = torch.FloatTensor([[1, 2]])
m2 = torch.FloatTensor([3]) # [3] -> [3, 3]
print(m1 + m2)
--------------------------------------------------------------------------------------------------------------------------------
tensor([[4., 5.]])

이번엔 (1, 2) 크기인 m1과 (2, 1) 크기인 m2와의 연산입니다. [[1, 2]]는 [[1, 2], [1, 2]]로, [[3], [4]]는 [[3, 3], [4, 4]]로 변환되어 계산됩니다.

m1 = torch.FloatTensor([[1, 2]])
m2 = torch.FloatTensor([[3], [4]])
print(m1 + m2)

# [1, 2]
# ==> [[1, 2],
#      [1, 2]]

# [3]
# [4]
# ==> [[3, 3],
#      [4, 4]]

--------------------------------------------------------------------------------------------------------------------------------
tensor([[4., 5.],
        [5., 6.]])

브로드캐스팅은 자동으로 수행되기 때문에 굉장히 편리한 기능이지만, 나중에 원하는 결과가 나오지 않았을 때 어디서 문제가 발생했는지 찾기가 굉장히 어려울 수 있다는 단점도 존재합니다. 따라서 주의하여 사용해야 합니다.


4. 행렬 곱셈과 곱셈의 차이 (Matrix Multiplication Vs. Multiplication)

matmul은 파이토치 텐서의 행렬 곱셈을 수행합니다.

m1 = torch.FloatTensor([[1, 2], [3, 4], [5, 6]])
m2 = torch.FloatTensor([[1], [2]])
print('Shape of Matrix 1 : ', m1.shape)
print('Shape of Matrix 2 : ', m2.shape)
# matmul : 행렬의 곱셈
print(m1.matmul(m2)) 
--------------------------------------------------------------------------------------------------------------------------------
Shape of Matrix 1 :  torch.Size([3, 2])
Shape of Matrix 2 :  torch.Size([2, 1])
tensor([[ 5.],
        [11.],
        [17.]])

행렬 곱셈이 아닌 element-wise 곱셈 (아마다르 곱셈)도 존재합니다. 동일한 크기의 행렬이 동일한 위치에 있는 원소끼리 곱하는 것을 말하는데 \* 또는 mul을 통해 수행합니다. 아래 예시는 브로드캐스팅을 수행한 뒤 아마다르 곱셈이 수행됩니다.

m1 = torch.FloatTensor([[1, 2], [3, 4], [5, 6]])
m2 = torch.FloatTensor([[1], [2], [3]]) # [[1], [2], [3]] -> [[1, 1], [2, 2], [3, 3]]
print('Shape of Matrix 1 : ', m1.shape)
print('Shape of Matrix 2 : ', m2.shape)
# mul : element-wise 곱셈
print("m1 * m2", m1 * m2)
print("m1.mul(m2)", m1.mul(m2))
--------------------------------------------------------------------------------------------------------------------------------
Shape of Matrix 1 :  torch.Size([3, 2])
Shape of Matrix 2 :  torch.Size([3, 1])
m1 * m2 tensor([[ 1.,  2.],
                [ 6.,  8.],
                [15., 18.]])
m1.mul(m2) tensor([[ 1.,  2.],
                   [ 6.,  8.],
                   [15., 18.]])


5. 평균 (Mean)

원소의 평균은 mean을 사용하여 구합니다.

t = torch.FloatTensor([10, 20])
print(t.mean())
--------------------------------------------------------------------------------------------------------------------------------
tensor(15.)

2차원 행렬에서도 평균을 구할 수 있습니다.

t = torch.FloatTensor([[5, 6], [7, 8]])
print(t)
print(t.mean())
--------------------------------------------------------------------------------------------------------------------------------
tensor([[5., 6.],
        [7., 8.]])
tensor(6.5000)

여기서 행렬의 행평균, 열평균을 구하기 위해서는 dim 인자를 사용해야 합니다. dim 인자를 주는 방법은 다음과 같습니다. $0$은 행, $1$은 열을 의미합니다. 여기서 dim이 지정하는 차원은 제거하는 차원을 의미합니다. 예를 들어 dim = 0은 행을 의미하므로 행이 없어지고 열평균이 도출됩니다.

print(t.mean(dim = 0)) # 0차원(행)을 제거하겠다. -> 열만 남음 
print(t.mean(dim = 1)) # 1차원(열)을 제거하겠다. -> 행만 남음
print(t.mean(dim = -1)) # 마지막 차원(열)을 제거하겠다. -> 행만 남음
--------------------------------------------------------------------------------------------------------------------------------
tensor([6., 7.])
tensor([5.5000, 7.5000])
tensor([5.5000, 7.5000])


6. 덧셈 (Sum)

덧셈은 sum을 이용하는 것 외에는 평균과 동일하게 구합니다.

t = torch.FloatTensor([[10, 20], [30, 40]])
print(t)
print(t.sum())
print(t.sum(dim = 0)) # 행을 제거
print(t.sum(dim = 1)) # 열을 제거
print(t.sum(dim = -1)) # 마지막 차원인 열을 제거
--------------------------------------------------------------------------------------------------------------------------------
tensor([[10., 20.],
        [30., 40.]])
tensor(100.)
tensor([40., 60.])
tensor([30., 70.])
tensor([30., 70.])


7. 최대 (Max)와 아그맥스 (ArgMax)

Max는 원소의 최댓값을 리턴하고, ArgMax는 최댓값을 가진 인덱스를 도출합니다. 앞에서 설명한 평균, 합계와 비슷하게 구현됩니다.

t = torch.FloatTensor([[50, 60], [70, 80]])
print(t)
print('-------------')
print(t.max())
print('-------------')
print(t.max(dim = 0)) # 행을 제거
print('-------------')
print(t.max(dim = 1)) # 열을 제거
print('-------------')
print(t.max(dim = -1)) # 열을 제거
print('-------------')
# [1, 1]의 의미 : argmax -> index 값을 말함
print('max : ', t.max(dim = 0)[0])
print('-------------')
print('Argmax : ', t.max(dim = 0)[1])
--------------------------------------------------------------------------------------------------------------------------------
tensor([[50., 60.],
        [70., 80.]])
-------------
tensor(80.)
-------------
torch.return_types.max(
values=tensor([70., 80.]),
indices=tensor([1, 1]))
-------------
torch.return_types.max(
values=tensor([60., 80.]),
indices=tensor([1, 1]))
-------------
torch.return_types.max(
values=tensor([60., 80.]),
indices=tensor([1, 1]))
-------------
max :  tensor([70., 80.])
-------------
Argmax :  tensor([1, 1])


다음 시간에 이어서 2장 내용을 설명드리겠습니다!


Reference

  1. Pytorch로 시작하는 딥러닝 입문
  2. THINK-PRO BLOG
  3. 지미뉴트론 개발일기


DATA_100%_LOGO_LIGHT



댓글남기기

참고

[연속형 분포] 코시 분포

안녕하세요! 최근 AI 기법들에 대해 설명 드렸었는데 잠시 쉬어가는 의미로 오랜만에 수리통계학 분포 시리즈로 돌아왔습니다. 올해 마지막 포스팅으로 코시 분포에 대해 설명드리도록 하겠습니다.

[Anomaly Detection] Isolation Forest

안녕하세요! 이번 시간에도 지난 포스트에 이은 Anomaly Detection 포스트입니다. 모델 기반 Anomaly Detection 기법 중 하나인 Isolation Forest에 대해 알아보도록 하겠습니다. 언뜻보면 Random Forest와 비슷한 부분도 있지만, 목적은...

[Anomaly Detection] LOF

이번 시간부터는 드디어 Anomaly Detection으로 넘어가보도록 하겠습니다. 평소에 이상탐지에 관심이 많았는데 재밌고 새로운 사실도 알게되서 너무 좋네요! 😄 Anomaly Detection 파트의 첫 번째 시간이기 때문에 간단히 이상탐지에 대해 알아보고, 밀도 기반 이...

[Sampling] Mixed sampling

이번 시간에는 Sampling의 마지막 포스트인 Mixed Sampling에 대해 알아보겠습니다. 즉, 앞서 설명드린 UnderSampling과 OverSampling을 모두 이용하는 Sampling 기법입니다. 간단히 2가지 정도를 소개하고 Sampling Chapter를 마...