[Time Series] 이중지수평활법
이번 포스트에서는 드디어 시계열 모형에 대해서 소개해 드리도록 하겠으며, 그 중 현업에서도 종종 사용되는 모델인 이중지수평활법에 대해 알아보도록 하겠습니다. 시계열에 대한 자세한 내용들은 생략하겠지만, 우선 지수평활법이 무엇인지 설명하고 이중지수평활법의 특징은 무엇인지, 실제 코딩 사용법 등 설명드리도록 하겠습니다.
개요
1. 지수평활법
지수평활법(Exponential Smoothing)은 시계열 통계 분석 기법 중 하나로, 독립변수 X가 아닌 종속변수 y 자체 값의 가중평균을 이용하여 미래의 y 값을 예측하는 기법입니다. 특히, 최근 데이터일수록 보다 많은 가중치를 주고, 과거 데이터일수록 가중치를 적게 두어 미래를 예측합니다. 이러한 지수평활법에는 여러가지가 있지만 이중 가장 간단한 단순지수평활법에 대해서 소개드리겠습니다. 단순지수평활법은 최근 데이터에 큰 가중치를 두어 가중평균을 구하는 단순한 방식의 기법입니다. $\alpha$는 가중치, $n$개의 $y$값이 존재하고 $y_i$가 $i$번째 $y$값이라고 할 때, 각 $t$시점의 $L$ 값을 아래와 같이 정의합니다.
$ \begin{align*} L_{0} &= y_{1} \\ L_{t+1} &= \alpha \cdot y_{t+1} + (1 - \alpha) \cdot L_{t},~~~t = 0, \dots, n \\ \end{align*}$
즉, $L$은 $y_{1}$부터 시작하여 점점 최근 데이터를 반영하는 쪽으로 계산됩니다. 아래와 같이 $t = 1$부터 $8$까지의 예시 데이터가 있을 때 $\alpha$ 값이 $0.2$라면, 다음과 같이 미래를 예측하는 것입니다.
| X (t 시점) | y (실제 값) | Level ($L_{t}$) |
|---|---|---|
| 0 | $L_{0} = 10$ | |
| 1 | 10 | $L_{1} = 0.2 * 10 + 0.8 * L_{0} = ~$$10$ |
| 2 | 30 | $L_{2} = 0.2 * 30 + 0.8 * L_{1} = ~$$14$ |
| 3 | 35 | $L_{3} = 0.2 * 35 + 0.8 * L_{2} = ~$$18.2$ |
| 4 | 25 | $L_{4} = 0.2 * 25 + 0.8 * L_{3} = ~$$19.56$ |
| 5 | 32 | $L_{5} = 0.2 * 32 + 0.8 * L_{4} = ~$$22.05$ |
| 6 | 40 | $L_{6} = 0.2 * 40 + 0.8 * L_{5} = ~$$25.64$ |
| 7 | 38 | $L_{7} = 0.2 * 38 + 0.8 * L_{6} = ~$$28.11$ |
| 8 | 34 | $L_{8} = 0.2 * 34 + 0.8 * L_{7} = ~$$29.29$ |
| 9 | 알 수 없음 | $L_{9} = ~$$29.29$ |
| 10 | 알 수 없음 | $L_{10} = ~$$29.29$ |
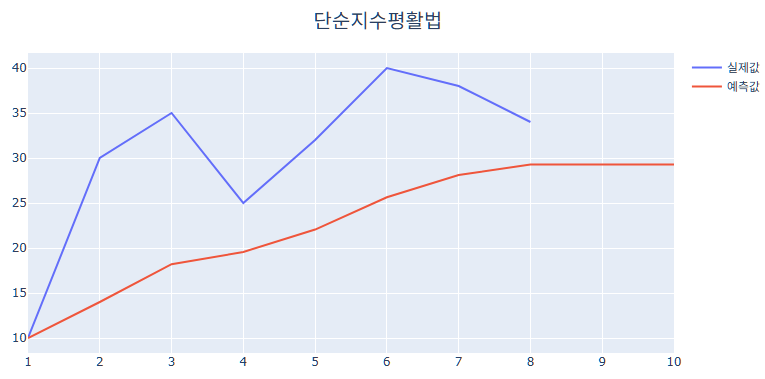
그러나 위와 같이 예측하고 싶은 미래시점과 관계 없이 예측값이 모두 $29.29$으로 동일하다는 한계, Trend나 Seasonal 변동이 있는 데이터에는 적합하지 않다는 한계로 단순지수평활법은 실생활에서 거의 사용되지 않습니다. 결론적으로 Trend 및 Seasonal 변동을 반영하여 분석해 줄 수 있는 시계열 기법이 필요합니다.
정의
2. 이중지수평활법
이중지수평활법을 설명하기 전, 시계열 분석에서 빠질 수 없는 Trend와 Seasonal에 대해 간단히 설명드리도록 하겠습니다.
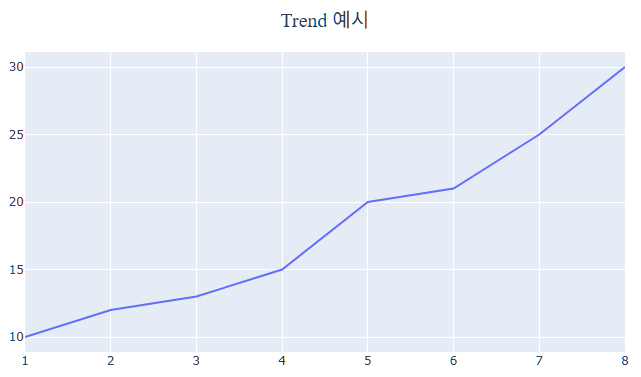
Trend는 추세변동을 의미합니다. 즉, 시간이 경과함에 따라 관측값이 지속적으로 증가/감소하는 변동을 의미하며 주로 경제지표과 관련된 데이터에서 발생됩니다.
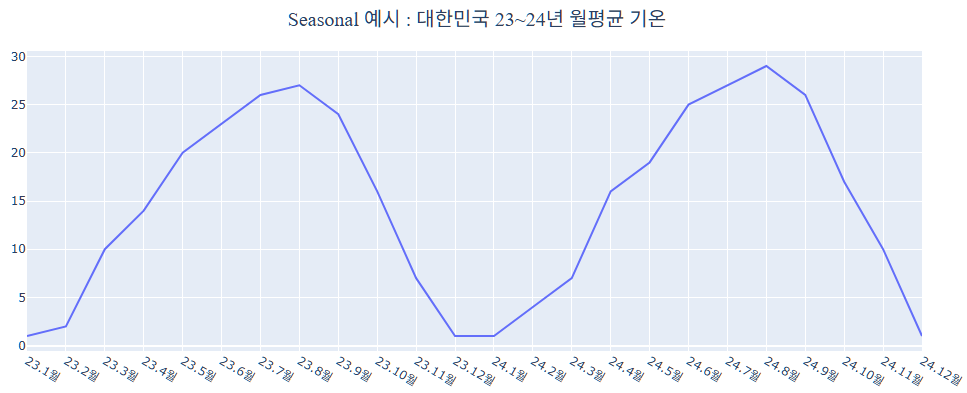
Seasonal는 계절변동을 의미합니다. 일별, 주별, 월별, 계절별과 같이 특정 주기 요인에 의한 변동을 의미합니다. 예시로 대한민국의 온도, 습도 변동이나, 제주도 관광객 수 변동이 이에 해당된다고 할 수 있습니다.
이 중 이중지수평활법은 Trend를 반영하여 단순지수평활법보다 한 단계 업그레이드 된 예측력을 가지게 됩니다. 즉, Trend가 존재하는 시계열 데이터 예측 시에 적합하며 단순지수평활법을 2번 적용하는 기법입니다. 아쉽게도 Season 변동은 반영되지 않습니다. 하지만, 재고관리, 매출예측 등 실생활의 단기적인 트렌드 분석에서 나름 잘 활용할 수 있는 기법입니다. 추세를 반영하기 때문에 단순지수평활법에 비해 더 현실적인 예측이 가능하며, 머신러닝 기법보다 계산이 간단하기 때문에 빠르게 예측할 수 있습니다.
이중지수평활법은 단순지수평활법을 2번 적용하는 기법으로 앞에서 말씀드렸을 겁니다. 이는 Trend(추세)와 Level(수준)을 따로 예측하기 때문입니다.
왜 예측에 Trend를 반영하면 좋고, Level과 따로 예측할까요? 예를 들어, 대한민국 2025.05.01 현재, 서울 최고 기온을 25도로 가정해보겠습니다. 여기서 Level은 현재의 평균 온도 상태 25도를 의미합니다. Trend는 이 온도가 앞으로 어떻게 변할 지에 대한 온도 증감을 의미합니다. 단순지수평활법은 최근 데이터에 가중치를 주며 현재 온도 25도를 중요하다고 말하지만, 미래에 온도가 어떻게 올라갈 지, 내려갈 지에 대한 변동을 반영하지 못합니다. 반면에 이중지수평활법은 Level에선 현재 온도에서의 기본 위치를 예측하고, Trend에서는 온도가 앞으로 어떻게 변동될 지를 따로 예측해서 Level + Trend * (예측 기간) 형태로 더 현실적인 미래 예측을 가능하게 합니다.
그렇다면, 값이 어떻게 구해지는지 알아보도록 하겠습니다. $\alpha, \beta$는 Level, Trend 각각의 가중치, $L_t$는 Level 예측값, $B_t$는 Trend 예측값이라고 할 때, 예측값 산출식은 아래와 같습니다.
$ \begin{align*} 1.~~&L_{0} : y_{1} \\ &B_{0} : y_{2} - y_{1} \\ \\ 2.~~&L_{t+1} = \alpha \cdot y_{t} + (1 - \alpha) \cdot (L_{t}+B_{t}),~~~t = 0, \dots, n \\ &B_{t+1} = \beta \cdot (L_{t+1}-L_{t}) + (1 - \beta) \cdot B_{t}, \\ \\ 3.~~&Forecast \\ &F_{t+h} = L_t + h \cdot B_{t} \\ \end{align*}$
우선 Level, Trend 초기값을 각각 $y_{1}, (y_{2}-y_{1})$로 구해집니다. $L_{t+1}$식에서 $y_t$는 최근 데이터, $(L_{t}+B_{t})$는 과거 데이터를 의미하므로 단순지수평활법과 비슷한 식임을 직관적으로 알 수 있습니다. $B_{t+1}$식에서 $(L_{t+1}-L_{t})$는 최근 데이터의 변동, $B_{t}$는 과거 데이터의 변동을 의미하므로 최근 데이터일수록 변동에 큰 가중치를 주는 식임을 알 수 있습니다. 이후 미래 예측값은 Level + Trend * (예측 기간)으로 도출하여 예측 기간에 따른 증감을 반영합니다. 이전 예시 데이터에 가중치를 모두 0.2로 두었을 때, 이중지수평활법을 적용해보겠습니다.
| X (t 시점) | y (실제 값) | Level ($L_{t}$) | Trend ($B_{t}$) | $\hat{y}$ (y 예측값 : $L_{t} + B_{t}$) |
|---|---|---|---|---|
| 0 | $L_{0} = 10$ | $B_{0} = 30 - 10 = 20$ | ||
| 1 | 10 | $L_{1} = 0.2 * 10 + 0.8 * (L_{0} + B_{0}) = ~$$26$ | $B_{1} = 0.2 * (26 - 10) + 0.8 * (B_{0}) = ~$$19.2$ | $\hat{y_1} = 10 + 20 = ~$$30$ |
| 2 | 30 | $L_{2} = 0.2 * 30 + 0.8 * (L_{1} + B_{1}) = ~$$42.16$ | $B_{2} = 0.2 * (42.16 - 26) + 0.8 * (B_{1}) = ~$$18.59$ | $\hat{y_2} = 26 + 19.2 = ~$$45.2$ |
| 3 | 35 | $L_{3} = ~$$55.60$ | $B_{3} = ~$$17.56$ | $\hat{y_3} = 42.16 + 18.59 = ~$$60.75$ |
| 4 | 25 | $L_{4} = ~$$63.53$ | $B_{4} = ~$$15.64$ | $\hat{y_4} = 55.60 + 17.56 = ~$$73.16$ |
| 5 | 32 | $L_{5} = ~$$69.73$ | $B_{5} = ~$$13.75$ | $\hat{y_5} = 63.53 + 15.64 = ~$$79.17$ |
| 6 | 40 | $L_{6} = ~$$74.79$ | $B_{6} = ~$$12.01$ | $\hat{y_6} = 69.73 + 13.75 = ~$$83.48$ |
| 7 | 38 | $L_{7} = ~$$77.04$ | $B_{7} = ~$$10.06$ | $\hat{y_7} = 74.79 + 12.01 = ~$$86.80$ |
| 8 | 34 | $L_{8} = ~$$76.47$ | $B_{8} = ~$$7.93$ | $\hat{y_8} = 77.04 + 10.06 = ~$$87.10$ |
| 9 | 알 수 없음 | $\hat{y_9} = 76.47 + 7.93 = ~$$84.40$ | ||
| 10 | 알 수 없음 | $\hat{y_{10}} = \hat{y_9} + 7.93 = ~$$92.33$ |
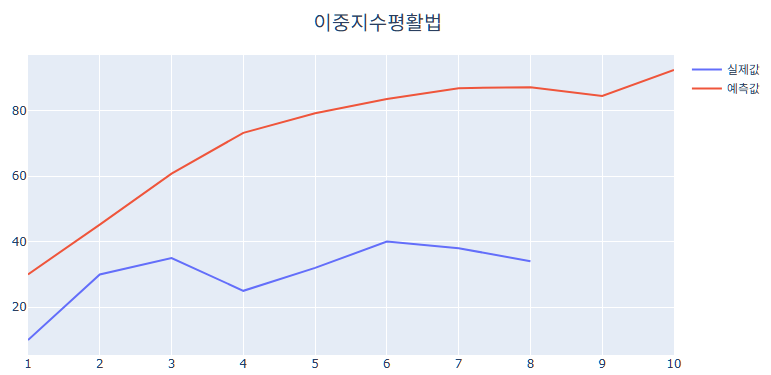
위와 같이 예측값을 구했지만, 생각보다 실제값과 비슷하게 적합되지 않은 것을 볼 수 있습니다. Trend 수준이 $0.2$와는 거리가 멀고, 데이터의 수도 적기 때문일 것으로 판단됩니다. 단순지수평활법과는 달리 예측하고 싶은 미래시점에 따라 예측값이 바뀌며, 추세를 반영하는 것을 알 수 있습니다.
실습
이번 실습 데이터는 대한민국의 Chocolate 구글 주간 검색량 추이 데이터를 분석해보도록 하겠습니다. 데이터 구성은 아래와 같습니다.
import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
from statsmodels.tsa.api import ExponentialSmoothing, Holt
from sklearn.metrics import mean_squared_error, mean_absolute_error
choco = pd.read_csv("~")
choco
- Shape : $(262, 2)$
- DATE : 주간일자
- COUNT : 구글 초콜릿 주간 검색량
먼저 Raw Data를 시각화 해보겠습니다. 과거에서 최근으로 가까워 질수록 점점 검색량이 올라가는 추이를 볼 수 있습니다.
fig = go.Figure()
fig.add_trace(go.Scatter(x = choco['DATE'], y = choco['COUNT'], mode = "lines", name = "실제값"), )
fig.update_layout(width = 800, height = 400, title_text = "대한민국 Chocolate 구글 주간 검색량", title_font_size = 20, title_x = 0.5, title_font_family = "Times New Roman",
margin_r = 50, margin_l = 50, margin_t = 50, margin_b = 50)
fig.show()
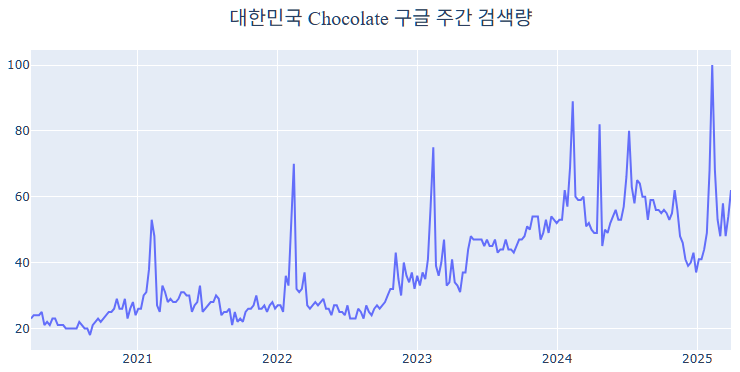
Raw Data를 Train과 Test로, 각각 200개, 62개의 Row로 나눕니다. 여기서 Train은 모델 적합을 할 수록 201개, 202개, …로 점점 늘어나게 됩니다.
train_data = choco.loc[: 200, :]
test_data = choco.loc[200 :, :]
print(test_data.shape)
--------------------------------------------------------------------------------------------------------------------------------
(62, 2)
이제 Train Data를 통해 미래 검색량을 예측하도록 하겠습니다. 예측 방법은 다음과 같습니다. 먼저 Train의 200개 데이터로 그 다음 주인 201번째 행의 검색량을 예측합니다. 이어서 Train을 201개로 끊은 뒤에 그 다음 주인 202번째 행의 검색량을 예측합니다. 이 과정을 반복하여 262번째까지의 예측값을 산출한 후, 실제 값과 비교해 보았습니다.
smoothing_trend는 자동으로 최적화된 값으로 정했으며, forecast(1)로 두어 다음 주의 값만 예측하도록 했습니다.
pred = []
for i in range(62) :
a_data = choco.loc[: (200 + i), :]
model = Holt(a_data['COUNT'], initialization_method = "estimated").fit()
result = model.forecast(1)
pred.append(result.to_list()[0])
test_data.loc[:, 'pred'] = pred
fig = go.Figure()
fig.add_trace(go.Scatter(x = test_data['DATE'], y = test_data['COUNT'], mode = "lines", name = "실제값"), )
fig.add_trace(go.Scatter(x = test_data['DATE'], y = test_data['pred'], mode = "lines",name = "예측값"), )
fig.update_layout(width = 800, height = 400, title_text = "이중지수평활법", title_font_size = 20, title_x = 0.5, title_font_family = "Times New Roman",
margin_r = 50, margin_l = 50, margin_t = 50, margin_b = 50)
fig.show()
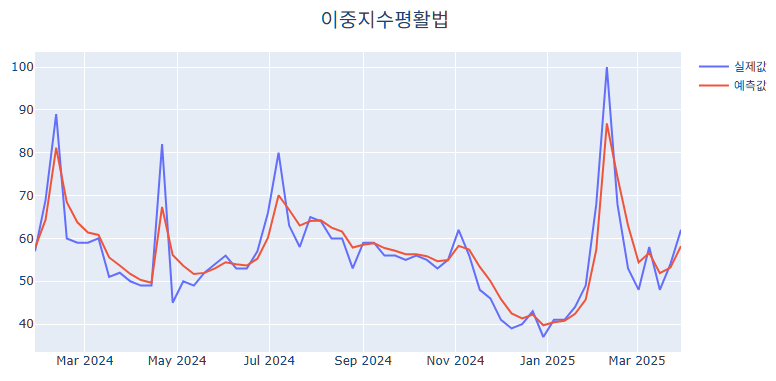
위 그래프를 보았을 때, 어느 정도 추세 경향성을 반영하여 예측하는 것으로 보이며, MSE, MAE 값도 적은 수치를 보이는 것을 알 수 있습니다.
print('MSE :', mean_squared_error(test_data['COUNT'], test_data['pred']))
print('MAE :', mean_absolute_error(test_data['COUNT'], test_data['pred']))
--------------------------------------------------------------------------------------------------------------------------------
MSE : 22.802347679977938
MAE : 3.3798630143591284
test_data

이어서 Trend와 Seasonal을 모두 반영해주는 기법인 Holt-Winters 계절성 기법에 대해 포스팅하도록 하겠습니다.
Reference

댓글남기기