[Time Series] Holt-Winters 계절성 기법
지난 포스트에서 시계열 모형의 기초적인 모델이라 말할 수 있는 지수평활법의 개념과 이중지수평활법에 대해 설명드렸다면, 이번 포스트에서는 그보다 한 단계 더 발전한 형태인 Holt-Winters 계절성 기법에 대해 설명드리도록 하겠습니다. 실제 데이터에 대해 이중지수평활법을 사용했을 때와 비교했을 때, 어떠한 차이가 있는지 알아보도록 하겠습니다.
개요
1. 이중지수평활법의 한계
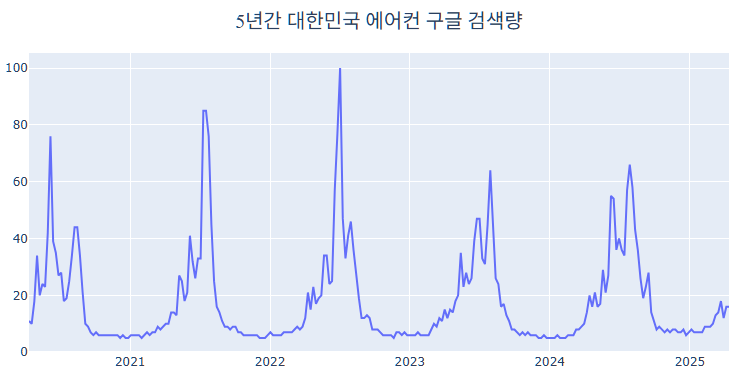
알다시피 이중지수평활법은 Trend를 반영하는 시계열 분석 기법으로, 실생활에서도 생각보다 예측력이 잘 맞는 기법입니다. 다만, 시계열 데이터의 구성요소 중 하나인 순환변동(Cycle)을 반영하지 않습니다. 한마디로, 순환변동의 일종이라 할 수 있는 Seasonal도 반영하지 않습니다. 때문에, 계절별/월별과 같이 어느 특정한 주기적인 요인이 데이터에 작용할 때는 적합하지 않을 수 있습니다. 예시로 5년 간 대한민국의 에어컨 구글 주간 검색량 데이터를 보면 매년 여름철에 급격하게 상승하는 계절적 요인을 볼 수 있는데, 이중지수평활법으로는 이러한 주기적인 변동을 반영하지 않은 채로 미래를 예측하여 성능이 떨어질 수 있습니다.
정의
2. Holt-Winters 계절성 기법(삼중지수평활법)
따라서, Trend뿐 아니라 Seasonal도 고려하는 시계열 분석 기법의 필요성이 대두됩니다. 그것이 바로 삼중지수평활법이라고 불리는 Holt-Winters 계절성 기법입니다. Holt-Winters 계절성 기법의 구성 요소는 이중지수평활법의 구성 요소인 Level(수준)과 Trend(추세)에 Seasonality(계절성)까지 더해집니다. 이 세 가지 요소를 결합하여 예측값을 만들어냅니다.
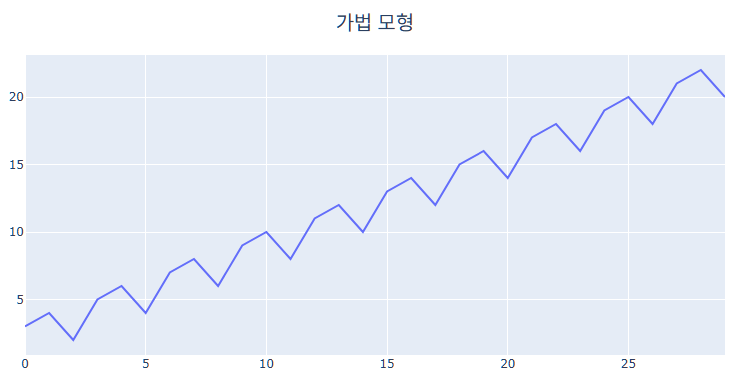
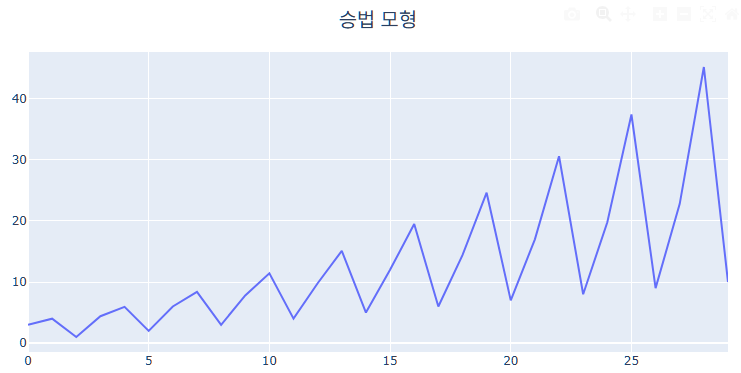
Holt-Winters 계절성 기법은 계절성이 데이터에 영향을 미치는 방식에 따라 Additive Model(가법 모형)과 Multiplicative Model(승법 모형)으로 나뉘게 되고, 예측값을 구하는 Logic도 살짝 달라지게 됩니다. 가법 모형은 계절성이 일정한 크기로 변하는 것으로 가정하고, 승법 모형은 계절성이 데이터의 크기에 비례하여 변화하는 것으로 가정합니다. 예를 들어, 콜라의 판매량이 매월 4천 개씩 증가한다는 것은 일정하게 판매되는 콜라 수가 더해지는 것이므로 가법 모형을 의미하지만, 매월 콜라의 판매량의 4%씩 증가한다는 것은 콜라의 판매량이 어느 비율만큼 곱해져서 증가한다는 것이므로 승법 모형을 의미하는 것입니다. 아래 그래프를 통해 비교해보면 이해가 될 것입니다.
가법 모형에서 예측값 산출식은 아래와 같습니다. 여기서 $h$는 미래 시점, $m$은 계절 주기, $k$는 주기적 반복 횟수를 의미합니다.
$ \begin{align*} \hat{y}_{t+h} &= L_{t} + h \cdot B_{t} + S_{t+h-m(k+1)} \\ \end{align*}$
추가 설명을 하자면, $m$은 데이터가 얼마나 자주 반복되는지, 즉 계절 패턴의 길이를 의미합니다. 월 데이터를 다룬다면 $m = 12$가 될 것이며, 주 데이터를 다룬다면 $m = 7$이 될 것입니다. $k$는 $h$가 $m$을 몇 번 넘겼는지, 즉 미래를 예측하는 시점이 계절 주기를 몇 번 넘겼는지를 의미합니다.
예시로 현재 시점이 25년 5월인데 예측 시점이 26년 9월이라고 가정해 보겠습니다. 이 때, $h=16$, 계절 주기는 $m = 12$가 될 것입니다. 주기적 반복 횟수는 16개월 = 1년 4개월이고, 주기를 한번 넘겼기 때문에 $k=1$이 됩니다. 따라서 $t$가 25년 5월 시점을 의미할 때, 아래와 같은 식이 만들어집니다.
$ \begin{align*} \hat{y}_{t+16} = L_{t} + 16 \cdot B_{t} + S_{t+16-12(1+1)} = L_{t} + 16 \cdot B_{t} + S_{t-8} \\ \end{align*}$
$S_{t-8}$라는 것은 현재 시점에서 8개월을 뺀 24년 9월의 계절성 요소를 참고한다는 것을 의미합니다.
승법 모형은 가법 모형과 산출식이 비슷하나, 계절성이 더해지지 않고, 곱해진다는 점에서 차이가 있습니다.
$ \begin{align*} \hat{y}_{t+h} &= (L_{t} + h \cdot B_{t}) \cdot S_{t+h-m(k+1)} \\ \end{align*}$
이어서 수준(Level), 추세(Trend), 계절성(Seasonality) 업데이트하는 방식에 대해서도 알아보겠습니다. 당연히 가법/승법에 따라 다르게 업데이트됩니다. 가법 모형에서는 덧셈을 사용하고, 승법 모형에서는 곱셈을 사용합니다. $\alpha, \beta, \gamma$는 각각 Level, Trend, Seasonality의 가중치, $L_t$는 Level 예측값, $B_t$는 Trend 예측값, $S_t$는 Seasonality 예측값을 의미합니다.
- (1) 수준(Level) 업데이트
- 가법 모형 : $L_t = \alpha(y_t-S_{t-m}) + (1-\alpha)(L_{t-1}+B_{t-1})$
- 승법 모형 : $L_t = \alpha \frac{y_t}{S_{t-m}} + (1-\alpha)(L_{t-1}+B_{t-1})$
- (2) 추세(Trend) 업데이트
- 가법 모형 : $B_t = \beta(L_t-L_{t-1}) + (1-\beta)B_{t-1}$
- 승법 모형 : $B_t = \beta \frac{L_t}{L_{t-1}} + (1-\beta)B_{t-1}$
- (3) 계절성(Seasonality) 업데이트
- 가법 모형 : $S_t = \gamma(y_t-L_{t}) + (1-\gamma)S_{t-m}$
- 승법 모형 : $S_t = \gamma \frac{y_t}{L_{t}} + (1-\gamma)S_{t-m}$
실습
그렇다면 Holt-Winters 계절성 기법의 가법모형과 승법모형을 실습을 통해 비교해보도록 하겠습니다. 데이터는 대한민국의 5년간 에어컨 구글 주간 검색량을 가져왔습니다. 데이터 구성은 아래와 같습니다.
import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from sklearn.metrics import mean_squared_error, mean_absolute_error
aircon = pd.read_csv("~")
aircon
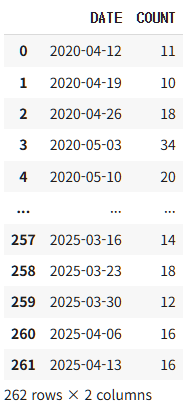
- Shape : $(262, 2)$
- DATE : 주간일자
- COUNT : 구글 에어컨 주간 검색량
먼저 Raw Data를 시각화해보면 연간 여름 시즌(6월~8월)이 될 때마다 크게 에어컨에 대한 검색량이 늘어나는 것을 알 수 있습니다. 즉, 연간 계절성(Seasonality)을 확연하게 볼 수 있습니다.
fig = go.Figure()
fig.add_trace(go.Scatter(x = aircon['DATE'], y = aircon['COUNT'], mode = "lines", name = "실제값"), )
fig.update_layout(width = 800, height = 400, title_text = "5년간 대한민국 에어컨 구글 검색량", title_font_size = 20, title_x = 0.5, title_font_family = "Times New Roman",
margin_r = 50, margin_l = 50, margin_t = 50, margin_b = 50)
fig.show()
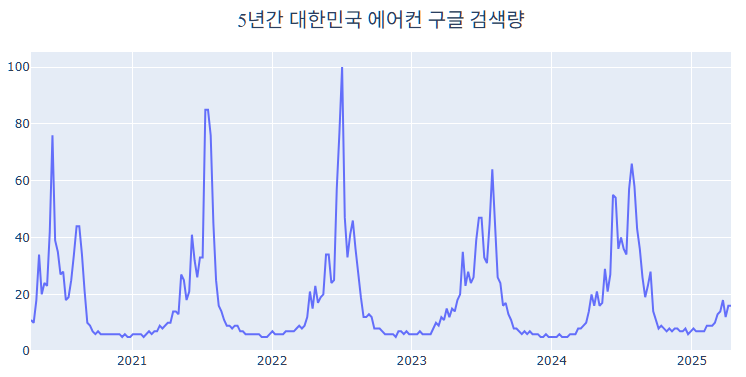
Raw Data를 Train과 Test로, 각각 200개, 62개의 Row로 나눕니다.
train_data = aircon.loc[: 200, :]
test_data = aircon.loc[200 :, :]
print(test_data.shape)
--------------------------------------------------------------------------------------------------------------------------------
(62, 2)
Holt-Winters 계절성 기법은 ExponentialSmoothing 함수를 통해 진행됩니다. 첫 번째로 가법모델을 적합시켜 보았습니다. seasonal_periods는 계절 주기인 $m$을 의미합니다. 즉, 데이터가 주간 데이터이기 때문에 $365 / 7 \fallingdotseq 52$로 두었습니다. 또한, Test 데이터인 62주만큼 예측을 진행합니다.
# 가법모델 (Additive)
add_model = ExponentialSmoothing(train_data['COUNT'], trend = 'add', seasonal = 'add', seasonal_periods = 52)
add_fit = add_model.fit()
add_forecast = add_fit.forecast(62)
파란색 선이 실제값, 빨간색 선이 Holt-Winters 계절성 기법을 통한 예측값을 의미하며, 실선은 Train, 점선은 Test 데이터를 의미합니다. 보시다시피 Holt-Winters 계절성 기법의 가법모형이 Test 데이터의 실제값과 비슷하게 예측한 것을 알 수 있습니다. 즉, 연간 계절성(Seasonality)을 잘 반영한 모델이 만들어졌습니다.
fig = go.Figure()
fig.add_trace(go.Scatter(x = train_data['DATE'], y = train_data['COUNT'], mode = "lines", name = "실제값"), )
fig.add_trace(go.Scatter(x = train_data['DATE'], y = add_fit.fittedvalues, mode = "lines", name = "예측값"), )
fig.add_trace(go.Scatter(x = test_data['DATE'], y = test_data['COUNT'], mode = "lines", name = "예측값", line_dash = 'dot', line_color = 'blue'), )
fig.add_trace(go.Scatter(x = test_data['DATE'], y = add_forecast, mode = "lines", name = "예측값", line_dash = 'dot', line_color = 'red'), )
fig.update_layout(width = 800, height = 400, title_text = "Holt-Winters 계절성 기법-Addictive", title_font_size = 20, title_x = 0.5, title_font_family = "Times New Roman",
margin_r = 50, margin_l = 50, margin_t = 50, margin_b = 50)
fig.show()
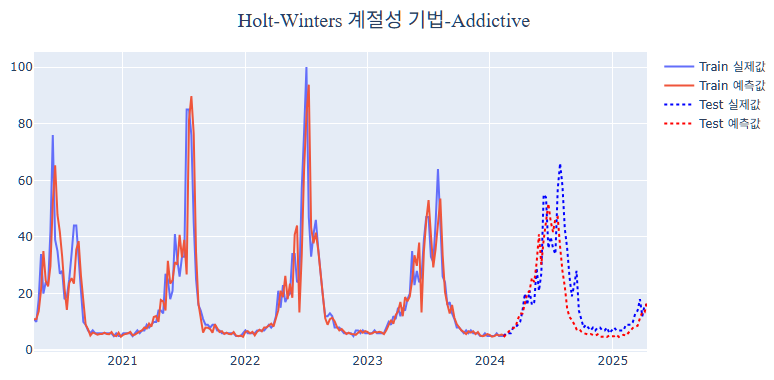
MSE, MAE 값도 적은 수치를 보이는 것을 알 수 있습니다.
print('MSE :', mean_squared_error(test_data['COUNT'], add_forecast))
print('MAE :', mean_absolute_error(test_data['COUNT'], add_forecast))
--------------------------------------------------------------------------------------------------------------------------------
MSE : 85.56772951001903
MAE : 6.009934110503207
두 번째로 아래와 같이 승법모델을 적합시켜 보았습니다.
# 승법모델 (Multiplicative)
mul_model = ExponentialSmoothing(train_data['COUNT'], trend = 'add', seasonal = 'mul', seasonal_periods = 52)
mul_fit = mul_model.fit()
mul_forecast = mul_fit.forecast(62)
Holt-Winters 계절성 기법의 승법모형은 계절성이 데이터의 크기에 비례하여 변화합니다. 다만 앞서 Raw Data를 보았을 때, 이 데이터는 계절성이 데이터의 크기에 비례하여 변하지는 않았습니다. 즉 승법모형이 어울리지 않는 데이터이며, 아래 시각화에서도 끝없이 상승하는 경향의 상당히 왜곡된 Test 예측값이 산출된 것을 알 수 있습니다.
fig = go.Figure()
fig.add_trace(go.Scatter(x = train_data['DATE'], y = train_data['COUNT'], mode = "lines", name = "Train 실제값"), )
fig.add_trace(go.Scatter(x = train_data['DATE'], y = mul_fit.fittedvalues, mode = "lines", name = "Train 예측값"), )
fig.add_trace(go.Scatter(x = test_data['DATE'], y = test_data['COUNT'], mode = "lines", name = "Train 실제값", line_dash = 'dot', line_color = 'blue'), )
fig.add_trace(go.Scatter(x = test_data['DATE'], y = mul_forecast, mode = "lines", name = "Test 예측값", line_dash = 'dot', line_color = 'red'), )
fig.update_layout(width = 800, height = 400, title_text = "Holt-Winters 계절성 기법-Multiplicative", title_font_size = 20, title_x = 0.5, title_font_family = "Times New Roman",
margin_r = 50, margin_l = 50, margin_t = 50, margin_b = 50)
fig.show()
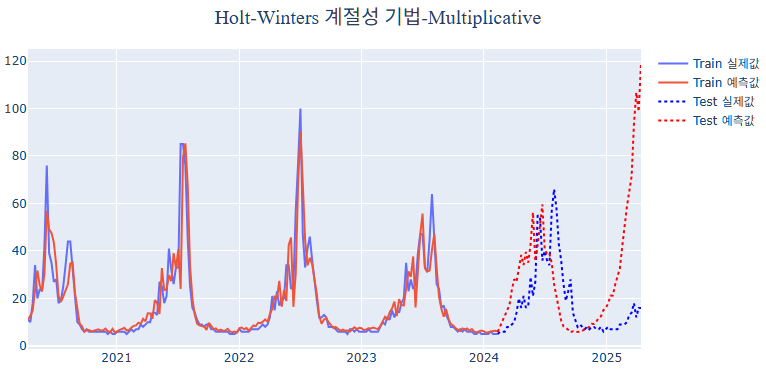
가법모형과 비교했을 때, MSE, MAE 값이 상당히 큰 것을 알 수 있었으며 해당 데이터는 Holt-Winters 계절성 기법의 가법모형에서 좋은 성능을 가지는 것을 알 수 있습니다.
print('MSE :', mean_squared_error(test_data['COUNT'], mul_forecast))
print('MAE :', mean_absolute_error(test_data['COUNT'], mul_forecast))
--------------------------------------------------------------------------------------------------------------------------------
MSE : 911.7516101460977
MAE : 19.979394701353787
Reference

댓글남기기